F E I J G H L K
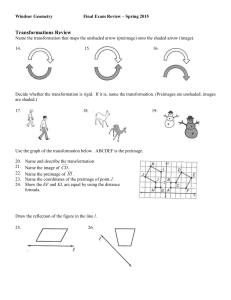
... STATE THE PROPERTY.) (do not use a protractor) Every answer should have a computation or a property listed. k List the angle measures in the order you find them. ...
... STATE THE PROPERTY.) (do not use a protractor) Every answer should have a computation or a property listed. k List the angle measures in the order you find them. ...
Document
... distance formulas d = a b segment addition postulate congruent congruence of segments construction: copy a segment construct a midpoint segment bisector ...
... distance formulas d = a b segment addition postulate congruent congruence of segments construction: copy a segment construct a midpoint segment bisector ...
3.6 Prove Theorems About Perpendicular Lines
... • If 2 lines intersect to form a linear pair of congruent angles, then the lines must be perpendicular. ...
... • If 2 lines intersect to form a linear pair of congruent angles, then the lines must be perpendicular. ...
Pretest - Reading Community Schools
... ____ 24. In a survey of a town, 56% of residents own a car, 21% of residents own a truck, and 4% of residents own both a car and a truck. What is the conditional probability that a person who owns a car also owns a truck? Round to the nearest whole number. A. 44% D. 7% B. 17% E. I don’t know. C. 19% ...
... ____ 24. In a survey of a town, 56% of residents own a car, 21% of residents own a truck, and 4% of residents own both a car and a truck. What is the conditional probability that a person who owns a car also owns a truck? Round to the nearest whole number. A. 44% D. 7% B. 17% E. I don’t know. C. 19% ...
Notes 6.4 – 6.6 6.4 Prove Triangles Similar by AA
... If the corresponding side lengths of two triangles are ____________________, then the triangles are similar. ...
... If the corresponding side lengths of two triangles are ____________________, then the triangles are similar. ...
Math Circle Beginners Group May 15, 2016 Geometry II
... exterior angle is supplementary to its adjacent interior angle. For every acute interior angle, there is an obtuse exterior angle. For every obtuse interior angle, there is an acute exterior angle. However, the exterior angles of a convex polygon add up to 360 , so at most 3 of the exterior angles c ...
... exterior angle is supplementary to its adjacent interior angle. For every acute interior angle, there is an obtuse exterior angle. For every obtuse interior angle, there is an acute exterior angle. However, the exterior angles of a convex polygon add up to 360 , so at most 3 of the exterior angles c ...
SamplePCXGeo
... 1. Draw triangles ABC and ADE with vertices having coordinates: A(0, 0), B(2, 0), C(5, 4), D(4, 5), E = (0, 8). Triangles are clearly not congruent, but they have some congruent parts. List all congruences you can find. 2. Construct triangle ABC such that AB = 3 and BC = 2, and ∠BAC = 30◦ . Is there ...
... 1. Draw triangles ABC and ADE with vertices having coordinates: A(0, 0), B(2, 0), C(5, 4), D(4, 5), E = (0, 8). Triangles are clearly not congruent, but they have some congruent parts. List all congruences you can find. 2. Construct triangle ABC such that AB = 3 and BC = 2, and ∠BAC = 30◦ . Is there ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑