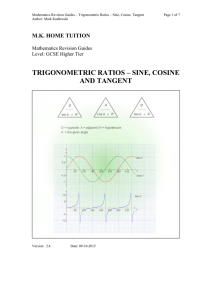
Geometry Seamless Curriculum Guide Geometry
... • Show congruency by using properties of coordinate geometry 3.3 The student will be able to prove and use triangular similarity. • Apply SSS (proportionality), AA Similarity, and SAS Similarity • Use ratios and proportions to find missing sides (indirect measurement) • Find geometric mean 3.4 The s ...
... • Show congruency by using properties of coordinate geometry 3.3 The student will be able to prove and use triangular similarity. • Apply SSS (proportionality), AA Similarity, and SAS Similarity • Use ratios and proportions to find missing sides (indirect measurement) • Find geometric mean 3.4 The s ...
Wizard Test Maker
... because division is evaluated before addition. (2) After evaluating 62, add 5 and then divide by 2 because addition is evaluated before division. (3) After evaluating 5 + 6, square it and then divide by 2 because addition is evaluated before both exponents and division. (4) The process of simplifyin ...
... because division is evaluated before addition. (2) After evaluating 62, add 5 and then divide by 2 because addition is evaluated before division. (3) After evaluating 5 + 6, square it and then divide by 2 because addition is evaluated before both exponents and division. (4) The process of simplifyin ...
Document
... 4. Name the corresponding congruent sides if LMN OPQ. LM OP; MN PQ; LN OQ 5. Find y if DEF is an equilateral triangle and mF = 8y + 4. ...
... 4. Name the corresponding congruent sides if LMN OPQ. LM OP; MN PQ; LN OQ 5. Find y if DEF is an equilateral triangle and mF = 8y + 4. ...
of your Geometry Textbook
... triangles (right, acute, scalene, isosceles, etc.) They prove that triangles are congruent or similar and use properties of these triangles to solve problems. G.1.1: Demonstrate understanding by identifying and giving examples of undefined terms, axioms, theorems, and inductive and deductive reasoni ...
... triangles (right, acute, scalene, isosceles, etc.) They prove that triangles are congruent or similar and use properties of these triangles to solve problems. G.1.1: Demonstrate understanding by identifying and giving examples of undefined terms, axioms, theorems, and inductive and deductive reasoni ...
Posnack Middle School summer Honors
... Identify Three-Dimensional Figures A solid with all flat surfaces that enclose a single region of space is called a polyhedron. Each flat surface, or face, is a polygon. The line segments where the faces intersect are called edges. The point where three or more edges meet is called a vertex. Polyhed ...
... Identify Three-Dimensional Figures A solid with all flat surfaces that enclose a single region of space is called a polyhedron. Each flat surface, or face, is a polygon. The line segments where the faces intersect are called edges. The point where three or more edges meet is called a vertex. Polyhed ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑