Review for Geometry End-of
... 70. Assume that is an acute angle and tan A = 1.230. The measure of is _____. a. about 39.1° b. about 7.01° c. about 50.9° d. about 129.9° 71. Find the missing angle and side measures of ABC, given that mA = 65°, mC = 90°, and CB = 15. a. B = 25°, c = 16.6, b = 7 b. B = 155°, c = 16.6, b = 7.5 c. ...
... 70. Assume that is an acute angle and tan A = 1.230. The measure of is _____. a. about 39.1° b. about 7.01° c. about 50.9° d. about 129.9° 71. Find the missing angle and side measures of ABC, given that mA = 65°, mC = 90°, and CB = 15. a. B = 25°, c = 16.6, b = 7 b. B = 155°, c = 16.6, b = 7.5 c. ...
Chapter 3 Vocabulary List - Brandywine School District
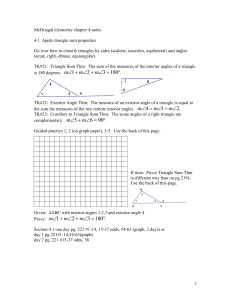
... Exterior Angle of a Triangle Theorem: The measure of an exterior angle of a triangle equals the sum of the measures of the two remote interior angles. Thrm: Each angle of an equiangular triangle has measure 60o . Thrm: The acute angles of a right triangle are complementary. ...
... Exterior Angle of a Triangle Theorem: The measure of an exterior angle of a triangle equals the sum of the measures of the two remote interior angles. Thrm: Each angle of an equiangular triangle has measure 60o . Thrm: The acute angles of a right triangle are complementary. ...
Solution of Sondow`s problem: a synthetic proof of the tangency
... Theorem 1. (Simson-Wallace Theorem) Given a triangle 4ABC and a point P in the plane, the orthogonal projections of P into the sides (also called pedal points) of the triangle are collinear if and only if P is on the circumcircle of 4ABC [2]. In general, a pedal curve is defined as the locus of orth ...
... Theorem 1. (Simson-Wallace Theorem) Given a triangle 4ABC and a point P in the plane, the orthogonal projections of P into the sides (also called pedal points) of the triangle are collinear if and only if P is on the circumcircle of 4ABC [2]. In general, a pedal curve is defined as the locus of orth ...
THE FARY-MILNOR THEOREM IN HADAMARD MANIFOLDS 1
... of variable curvature. The question of whether the Fary-Milnor Theorem can be extended to general nonpositively curved manifolds recently arose in several quarters. If Hadamard manifolds are in fact the right setting for this theorem, it seems that another essentially different proof is needed. Inte ...
... of variable curvature. The question of whether the Fary-Milnor Theorem can be extended to general nonpositively curved manifolds recently arose in several quarters. If Hadamard manifolds are in fact the right setting for this theorem, it seems that another essentially different proof is needed. Inte ...
MPP1D1
... I – A line dividing an angle into 2 equal parts. J – A line perpendicular to the side of a triangle through its midpoint. K – A circle constructed using the circumcentre as the centre, that passes through each vertex of the triangle. L – A circle inside a triangle. It is constructed using the incent ...
... I – A line dividing an angle into 2 equal parts. J – A line perpendicular to the side of a triangle through its midpoint. K – A circle constructed using the circumcentre as the centre, that passes through each vertex of the triangle. L – A circle inside a triangle. It is constructed using the incent ...
Number Algebra Shape, space and measures Handling data G write
... 20, 17, 12, ...... go into negative Matchsticks pattern. Given 3 diagrams, how many needed for diagram 5? Explain write down the 5th line in pattern: 112-102=21, 10292=..., 92-..., output from 2-operation rule: input -2 , add 5 , mult. by 2 which of 'always even', 'always odd', 'could be odd or even ...
... 20, 17, 12, ...... go into negative Matchsticks pattern. Given 3 diagrams, how many needed for diagram 5? Explain write down the 5th line in pattern: 112-102=21, 10292=..., 92-..., output from 2-operation rule: input -2 , add 5 , mult. by 2 which of 'always even', 'always odd', 'could be odd or even ...
Convex Sets and Convex Functions on Complete Manifolds
... If the sectional curvature K of M is nonnegative everywhere, then it follows from Toponogov's triangle comparison theorem that Fy is convex. Obviously it is not constant on any open set of M. Moreover the function F: M^R defined to be F(x) = sup[Fy(x); y(0)=p] is convex and exhaustion, where the sup ...
... If the sectional curvature K of M is nonnegative everywhere, then it follows from Toponogov's triangle comparison theorem that Fy is convex. Obviously it is not constant on any open set of M. Moreover the function F: M^R defined to be F(x) = sup[Fy(x); y(0)=p] is convex and exhaustion, where the sup ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑