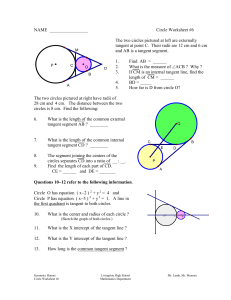
Parallelograms (part 2)
... Ways to Prove a Quadrilateral is a Parallelogram Ø Show both pairs of opposite sides are parallel. Ø Show both pairs of opposite sides are congruent. Ø Show both pairs of opposite angles are congruent. Ø Show one angle is supplementary to both consecutive angles. Ø Show the diagonals bise ...
... Ways to Prove a Quadrilateral is a Parallelogram Ø Show both pairs of opposite sides are parallel. Ø Show both pairs of opposite sides are congruent. Ø Show both pairs of opposite angles are congruent. Ø Show one angle is supplementary to both consecutive angles. Ø Show the diagonals bise ...
MA106 - Mohawk Valley Community College
... Graphing Trigonometric Functions by plotting points: This might be used to introduce 14.1, calculating and plotting points, and then followed by frequency and period examples from the text. y = a sin bx and y = a cos bx: Colored pencils are helpful (and may be found in AB208 cabinet or file drawers) ...
... Graphing Trigonometric Functions by plotting points: This might be used to introduce 14.1, calculating and plotting points, and then followed by frequency and period examples from the text. y = a sin bx and y = a cos bx: Colored pencils are helpful (and may be found in AB208 cabinet or file drawers) ...
Goemetry Gallery and Coordinate Geometry
... Proof: logical reasoning that uses facts, definitions, properties, and previously proven theorems to show that a proposition is true Syllogism (SIH-luh-jih-zuhm): a logical argument that always contains two premises and a conclusion; syllogisms have the following form: If a, then b. If b, then c. Th ...
... Proof: logical reasoning that uses facts, definitions, properties, and previously proven theorems to show that a proposition is true Syllogism (SIH-luh-jih-zuhm): a logical argument that always contains two premises and a conclusion; syllogisms have the following form: If a, then b. If b, then c. Th ...
Chapter 1
... Euclid says, “To extend a finite straight line continuously in a straight line.” In modern times it is often paraphrased as, “A straight line can be extended indefinitely in either direction,” and the parallel postulate does not make much sense without this understanding. Presumably Greenberg has st ...
... Euclid says, “To extend a finite straight line continuously in a straight line.” In modern times it is often paraphrased as, “A straight line can be extended indefinitely in either direction,” and the parallel postulate does not make much sense without this understanding. Presumably Greenberg has st ...
Analytic geometry
In classical mathematics, analytic geometry, also known as coordinate geometry, or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.Analytic geometry is widely used in physics and engineering, and is the foundation of most modern fields of geometry, including algebraic, differential, discrete and computational geometry.Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and squares, often in two and sometimes in three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space (three dimensions). As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometrical shapes in a numerical way and extracting numerical information from shapes' numerical definitions and representations. The numerical output, however, might also be a vector or a shape. That the algebra of the real numbers can be employed to yield results about the linear continuum of geometry relies on the Cantor–Dedekind axiom.