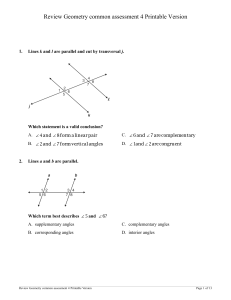
2nd Unit 3: Parallel and Perpendicular Lines
... Compare the methods Big Ideas Geometry coordinates of a point of a point that is given along the directed line segment AB Coplanar of counting lines on the 3.5, Example 2 that is a given fractional fractional distance from so that AP to PB is the ratio 2 to 6 Distance Formula number line or distance ...
... Compare the methods Big Ideas Geometry coordinates of a point of a point that is given along the directed line segment AB Coplanar of counting lines on the 3.5, Example 2 that is a given fractional fractional distance from so that AP to PB is the ratio 2 to 6 Distance Formula number line or distance ...
HOMEWORK ASSIGNMENT #6 SOLUTIONS
... 1. (Exercises 9.1.22 — 9.1.27, page 369) It can be proved that each of the statements in Exercise 22–27 is equivalent to Euclid’s fifth postulate. Rewrite each sentence, using the negation of the conclusion, to give a statement assume to be true in non-Euclidean geometry. 9.1.22: If a straight line ...
... 1. (Exercises 9.1.22 — 9.1.27, page 369) It can be proved that each of the statements in Exercise 22–27 is equivalent to Euclid’s fifth postulate. Rewrite each sentence, using the negation of the conclusion, to give a statement assume to be true in non-Euclidean geometry. 9.1.22: If a straight line ...
Test #1 Review
... Short answer or fill-in-the-blank, State certain definitions, theorems, postulates. Compute various numbers, figures, correspondences, and equations using the concepts we have studied (e.g., congruence of triangles, and the Poincare Half-plane model of Hyperbolic Geometry). Understand the proofs pre ...
... Short answer or fill-in-the-blank, State certain definitions, theorems, postulates. Compute various numbers, figures, correspondences, and equations using the concepts we have studied (e.g., congruence of triangles, and the Poincare Half-plane model of Hyperbolic Geometry). Understand the proofs pre ...
Standards
... linear and quadratic functions, and simple rational and exponential functions.★ MCC9-12.A.CED.2 Create equations in two or more variables to represent relationships between quantities; graph equations oncoordinate axes with labels and scales.★ (Focus on quadratic functions; compare with linear and e ...
... linear and quadratic functions, and simple rational and exponential functions.★ MCC9-12.A.CED.2 Create equations in two or more variables to represent relationships between quantities; graph equations oncoordinate axes with labels and scales.★ (Focus on quadratic functions; compare with linear and e ...
Unit 1 Conjectures
... Linear Pair Conjecture: If two angles form a linear pair, then _____________________________________________________________. Vertical Angles Conjecture: If two angles are vertical angles, then ______________________________________________________. Parallel Lines Conjecture: If two parallel lines a ...
... Linear Pair Conjecture: If two angles form a linear pair, then _____________________________________________________________. Vertical Angles Conjecture: If two angles are vertical angles, then ______________________________________________________. Parallel Lines Conjecture: If two parallel lines a ...
January Regional Geometry Team: Question #1 Points P, Q, R, S
... Let Y = the number of sides of a regular polygon that has interior angle measures of 168 degrees. Let Z = the number of sides of a regular polygon that has exterior angle measures of 18 degrees. Let A = the number of letters in the point of concurrency defined by the intersection of the altitudes of ...
... Let Y = the number of sides of a regular polygon that has interior angle measures of 168 degrees. Let Z = the number of sides of a regular polygon that has exterior angle measures of 18 degrees. Let A = the number of letters in the point of concurrency defined by the intersection of the altitudes of ...
Analytic geometry
In classical mathematics, analytic geometry, also known as coordinate geometry, or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.Analytic geometry is widely used in physics and engineering, and is the foundation of most modern fields of geometry, including algebraic, differential, discrete and computational geometry.Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and squares, often in two and sometimes in three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space (three dimensions). As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometrical shapes in a numerical way and extracting numerical information from shapes' numerical definitions and representations. The numerical output, however, might also be a vector or a shape. That the algebra of the real numbers can be employed to yield results about the linear continuum of geometry relies on the Cantor–Dedekind axiom.