* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download MYP 4 Mathematics 9
Analytic geometry wikipedia , lookup
Noether's theorem wikipedia , lookup
Multilateration wikipedia , lookup
Euclidean geometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Quadratic form wikipedia , lookup
Rational trigonometry wikipedia , lookup
Integer triangle wikipedia , lookup
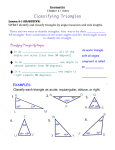
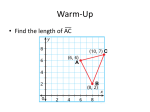
MYP 4 Ms. Lesley Ballew Room 405 [email protected] (808) 261-0707 x2160 Mathematics 9 Mr. Joshua Lyons Room 404 [email protected] (808) 261-0707 x2310 MYP 4 Integrated Math will focus primarily on topics from both Algebra and Geometry. The course will stress the essential role of mathematics within the school and in society: mathematics as a universal language, promoting analytical reasoning and problem-solving skills that contribute to the development of logical, abstract, and critical thinking. This course will help students view mathematics as a language of modeling and solving problems that arise in the real world. 2014 – 2015 Scope and Sequence: August-December All Unit Dates are projected and may be subject to change. You will be sent a January-May Scope and Sequence in January. Unit 1: Triangles in Design Late Aug- Mid Oct Key concept: Logic Related concepts(s): Justification, Generation Global context: Scientific and Technical Innovation: Engineering Inquiry statement: To justify engineering decisions we can use logical reasoning to arrive at general conclusions. Inquiry questions: Factual: What justification is needed in order to prove two triangles are congruent? What are the relationships between the angle measures and the side lengths of a triangle? What relationship must three line segments have with each other to form a triangle? Conceptual: Why does a rectangular gate become more stable when a diagonal is added on to it? Why is a general theorem a more valid justification than a statement specific to a problem? Debatable: Is there one best way to construct a proof or convincing argument? Content • Know: Properties of triangles, classifying triangles, solving triangles, proving congruency, and writing conditional statements. • Understand: How to apply the previously stated concepts to engineering tasks. • Do: Construct a valid and convincing argument, use conditional logic to prove triangles are congruent, and build a bridge using triangular construction. Summative Assessment Task(s) • Bridge Project (Crit. D) • Unit Test (Crit. A, C) Unit 2: Exponents Mid Oct- Late Nov Key concept: Logic Related concepts(s): Simplification, System Global context: Personal and Cultural Expression: Metacognition and abstract thinking Inquiry statement: Simplification requires an understanding and logical application of rules within a system. Inquiry questions: Factual: What are the Laws of Exponents? Conceptual: How does expressing values in Scientific Notation make them easier to work with in scientific and technological fields? Debatable: Is it always better to be exact when expressing a number, value, or quantity? Content • Know: There are multiple forms for representing a number (integers, fractions, decimals, exponents, Scientific Notation, absolute value, radicals) • Understand: Radical expressions can be simplified, the relationship of Number Sets • Do: Evaluate numbers with integer exponents, derive and use the Laws of Exponents, simplify radical expressions Summative Assessment Task(s) • Investigation- Towers of Hanoi (Crit. B) • Presentation- Teaching the Laws of Exponents (Crit. A, C) • Unit Test (Crit. A) Unit 3: Right Triangles and the Sun Late Nov- Jan Key concept: Relationships Related concepts(s): Model, Measurement Global context: Globalization and Sustainability: Natural Resources Inquiry statement: Our relationship to finite natural resources motivates innovators to develop and assess sustainable models for utilizing renewable power. Inquiry questions: Factual: What are the relationships between the side lengths of a right triangle? What makes two figures similar? How can we measure the distance between two points on a coordinate plane? Conceptual: Why does SOH-CAH-TOA only work on right triangles? How does the sun allow us to measure the height of an object? Debatable: Can solar energy be a sustainable replacement of fuel energy in Hawaii? Content • Know: Properties of similar figures, Pythagorean Theorem, distance formula, Special Right triangles, Right Triangle Trigonometry. • Understand: All right triangles have the same relationship between the side lengths, angle of elevation and depression, and trigonometric ratios. • Do: Calculate missing measures of a right triangle given different combinations of information and to construct a solar oven assessed with right triangle trigonometry. Summative Assessment Task(s) • Build and Asses Solar Ovens (Crit. D) • Investigation of Patterns and Special Right Triangles (Crit. B) • Unit Test (Crit. A) Unit 3: Right Triangles and the Sun January – late February Key concept: Relationships Related concepts: Measurement, Model Global context: Globalization and Sustainability (consumption, conservation, natural resources and public goods) Statement of inquiry: Our relationship to finite natural resources motivates innovators to develop and assess sustainable models for utilizing renewable power. Inquiry questions: Factual: What are the relationships between the lengths of sides of a right triangle? What makes two figures similar? Conceptual: Why does SOH-CAH-TOA only work for right triangles? How does the sun allow us to measure the height of an object? Debatable: Can solar energy be a sustainable replacement of fuel energy in Hawaii? Content • Know: similar triangles; the Pythagorean Theorem; special right triangles; right triangle trigonometry (SOH CAH TOA); angles of elevation and depression • Understand: Similar triangles have proportional sides and congruent angles. The sides of a right triangle are always in the relationship of the Pythagorean Theorem. Right triangles can be solved using trigonometric ratios (SOH CAH TOA). The angles of elevation and depression are congruent. • Do: verify two triangles are similar; use the Pythagorean Theorem to solve for a missing side length in a right triangle; use the Pythagorean Theorem to classify a triangle by its angles; solve for missing side lengths or angle measures in a right triangle using trigonometric ratios; find the height of an object using similarity, Pythagorean Theorem, and trigonometric ratios; interpret the relationship between the angle of elevation of the sun and solar efficiency. Summative Assessment Tasks • Investigating Patterns in Special Right Triangles (Crit. B) • • • Solar Oven Project (Crit. C, D) Mid-Unit Summative Test (Crit. A) End of Unit Summative Test (Crit. A) Unit 4: Quadrilaterals March-early April Key concept: Relationships Related concepts: Measurement, Justification Global context: Scientific and Technical Innovation (mathematical puzzles, principles and discoveries) Statement of inquiry: Relationships, such as measurement and congruence, can be used to justify the classification of specific objects into a group. Inquiry questions: Factual: What are the defining features of parallelograms, rhombi, rectangles, squares, trapezoids, isosceles trapezoids, and kites? What are the area formulas for each of these quadrilaterals? Conceptual: How can distance formula and the slope of a line serve as evidence for classifying quadrilaterals? How is it possible that different shaped quadrilaterals have the same area formulas? Debatable: Is using the slopes of lines a valid proof for classifying a quadrilateral? Content • Know: Properties of parallelograms, rhombi, rectangles, squares, trapezoids, isosceles trapezoids, and kites; corresponding Area formulas; the distance formula • Understand: The relationships of quadrilaterals can be illustrated using a Venn diagram; the area of all parallelograms can be found using the same formula • Do: Use slope and the distance formula to justify the classification of quadrilaterals; Calculate the area of a variety of quadrilaterals Summative Assessment Task(s) • Classifying Quadrilaterals using Coordinate Proof (Crit. C) • Unit Test (Crit. A) Unit 5: Putting on the Breaks April-May Key concept: Relationships Related concepts: Change, Model Global context: Orientation in space and time (scale, duration, frequency, variability) Statement of inquiry: Modeling helps to demonstrate relationships between variables, and can be the driving force in change of policy or design. Inquiry questions: Factual: How many zeros can a quadratic equation have? Conceptual: Is every quadratic expression factorable? How can quadratic equations be used to model stopping distances? Debatable: Is there a best method to solve a quadratic equation? Content • Know: the distributive property for multiplying polynomials; quadratic equations can have zero, one or two real solutions; quadratic equations can be solved by factoring, graphing on a GDC (graphic display calculator), and the quadratic formula • Understand: the FOIL method for multiplying binomials is the distributive property; the x-intercepts of the graph of a quadratic function are the solutions to the equation when set equal to zero; all quadratic equations can be solved by using the quadratic formula; quadratic functions can be used to calculate and model many real world situations • Do: factor binomial and trinomial expressions; solve quadratic equations by factoring, graphing on a GDC, and the quadratic formula, calculate the breaking distance of different vehicles Summative Assessment Task(s) • Investigation into factoring special cases (Crit. B) • Explore breaking distances (Crit. D) • Unit Test (Crit. A) Mathematics Grading Criteria A. Knowing and Understanding B. Investigating Patterns C. Communicating D. Applying Mathematics in Real-Life Contexts Achievement Levels 0-8 0-8 0-8 0-8 Please refer to the MYP Parent Assessment Handbook for more information on MYP grading. You are also welcome to contact me, Vicki McNeill (HS Principal), Damian Rentoule (MS Principal), or Diane Smith (MYP Coordinator) with any questions about the MYP grading philosophy and practices. Office hours: Students are encouraged to use study hall or lunch/recess to receive extra learning support. In addition, afterschool meetings can be arranged dependent upon scheduled faculty meetings.