BGJHS
... 8.F.2 Compare properties of two functions each represented in a different way (algebraically, graphically, numerically in tables, or by verbal descriptions). For example, given a linear function represented by a table of values and a linear function represented by an algebraic expression, determine ...
... 8.F.2 Compare properties of two functions each represented in a different way (algebraically, graphically, numerically in tables, or by verbal descriptions). For example, given a linear function represented by a table of values and a linear function represented by an algebraic expression, determine ...
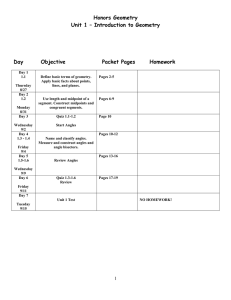
2.7 Angle Pair Relationships
... The graph shown represents a hyperbola. Draw the solid of revolution formed by rotating the hyperbola around the y-axis. ...
... The graph shown represents a hyperbola. Draw the solid of revolution formed by rotating the hyperbola around the y-axis. ...
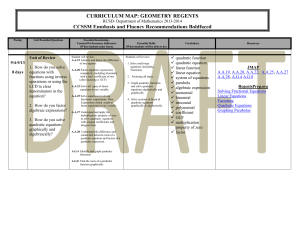
TN Geometry Traditional Pacing Guide 2017-18
... Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. Represent transformations in the plane using transparencies and geometry software; describe transf ...
... Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. Represent transformations in the plane using transparencies and geometry software; describe transf ...
Document
... In solving inequalities, the solution process is very similar to solving equations. The goal is still to isolate the variable, to get the letter by itself. However, the one difference between equations and inequalities is that when solving inequalities, when we multiply or divide by a negative numbe ...
... In solving inequalities, the solution process is very similar to solving equations. The goal is still to isolate the variable, to get the letter by itself. However, the one difference between equations and inequalities is that when solving inequalities, when we multiply or divide by a negative numbe ...
Student Overview Sheet Standards GC
... G-F-TF-2 Explain how the unit circle in the coordinate plane enables the extension of trigonometric functions to all real numbers, interpreted as radian measures of angles traversed counterclockwise around the unit circle. G-C-2 Identify and describe relationships among inscribed angles, radii, and ...
... G-F-TF-2 Explain how the unit circle in the coordinate plane enables the extension of trigonometric functions to all real numbers, interpreted as radian measures of angles traversed counterclockwise around the unit circle. G-C-2 Identify and describe relationships among inscribed angles, radii, and ...
Document
... Find the distance between these 2 points and the slope. Graph this circle, indicating the center, radius and 6 points on the circle. Find the lengths of all three sides of RST. Use the converse of the Pythagorean Theorem to show that RST is a right triangle. Show two of the sides have perpendicu ...
... Find the distance between these 2 points and the slope. Graph this circle, indicating the center, radius and 6 points on the circle. Find the lengths of all three sides of RST. Use the converse of the Pythagorean Theorem to show that RST is a right triangle. Show two of the sides have perpendicu ...
Parallel Postulate
... In Riemannian geometry, geometric shapes such as triangles have a different appearance than what they would in Euclidean geometry. A spherical triangle may have sides that curvature which would allow these triangles to have some special properties. For example a spherical triangle can have more one ...
... In Riemannian geometry, geometric shapes such as triangles have a different appearance than what they would in Euclidean geometry. A spherical triangle may have sides that curvature which would allow these triangles to have some special properties. For example a spherical triangle can have more one ...
ROCKY FORD CURRICULUM GUIDE SUBJECT: Geometry GRADE
... solve problems involving right triangles. i. Explain that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles. C ...
... solve problems involving right triangles. i. Explain that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles. C ...
Analytic geometry
In classical mathematics, analytic geometry, also known as coordinate geometry, or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.Analytic geometry is widely used in physics and engineering, and is the foundation of most modern fields of geometry, including algebraic, differential, discrete and computational geometry.Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and squares, often in two and sometimes in three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space (three dimensions). As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometrical shapes in a numerical way and extracting numerical information from shapes' numerical definitions and representations. The numerical output, however, might also be a vector or a shape. That the algebra of the real numbers can be employed to yield results about the linear continuum of geometry relies on the Cantor–Dedekind axiom.