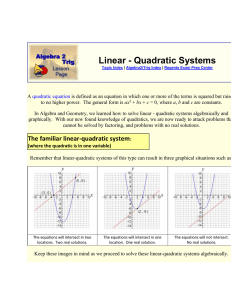
Systems of Equations: E.g. 2x + 3y = 1 x
... Once we found the value of y, we may substitute it into any of the two equations to solve for x: 2x + 3(−1) = 1 2x − 3 = 1 2x = 4 x=2 The solution is (2, −1), notice that the solution is an ordered pair. ...
... Once we found the value of y, we may substitute it into any of the two equations to solve for x: 2x + 3(−1) = 1 2x − 3 = 1 2x = 4 x=2 The solution is (2, −1), notice that the solution is an ordered pair. ...
4-5 & 6, Factor and Remainder Theorems revised
... that there are 4 roots. They may be real, imaginary or complex. The Rational Root Theorem identifies possible rational roots. p = 18 and q = 1 ...
... that there are 4 roots. They may be real, imaginary or complex. The Rational Root Theorem identifies possible rational roots. p = 18 and q = 1 ...
test 1
... 12. Solve the inequality: 500 − 2x ≥ x + 140 13. A bartender wants to mix a 5% alcohol solution with 25% alcohol solution to obtain two liters of a 10% alcohol solution. How much of the weaker and how much of the stronger ...
... 12. Solve the inequality: 500 − 2x ≥ x + 140 13. A bartender wants to mix a 5% alcohol solution with 25% alcohol solution to obtain two liters of a 10% alcohol solution. How much of the weaker and how much of the stronger ...
No Slide Title
... complex roots, the possible number of real roots, and the possible rational roots. By the corollary to the Fundamental Theorem of Algebra, x4 – 3x3 + 4x + 1 = 0 has four complex roots. By the Imaginary Root Theorem, the equation has either no imaginary roots, two imaginary roots (one conjugate pair) ...
... complex roots, the possible number of real roots, and the possible rational roots. By the corollary to the Fundamental Theorem of Algebra, x4 – 3x3 + 4x + 1 = 0 has four complex roots. By the Imaginary Root Theorem, the equation has either no imaginary roots, two imaginary roots (one conjugate pair) ...
Solving Multi-Step Equations - MELT-Institute
... Multiplicative inverses are two numbers that when multiplied together equal 1. When you multiply a term with a fractional coefficient by the multiplicative inverse of the fraction, you can isolate the variable on one side of the equation. This is known as multiplying by the reciprocal. When you mult ...
... Multiplicative inverses are two numbers that when multiplied together equal 1. When you multiply a term with a fractional coefficient by the multiplicative inverse of the fraction, you can isolate the variable on one side of the equation. This is known as multiplying by the reciprocal. When you mult ...
MIDTERM 2 SOLUTIONS 1. Consider the following function: f(x, y
... interest compounded continuously at the annual rate of 5%, and each year $1000 is continuously withdrawn. Set up a differential equation that A(t) satisfies, and specify the initial condition on A(t). Do not solve the differential equation. Solving the equation, even if correct, will not receive any ...
... interest compounded continuously at the annual rate of 5%, and each year $1000 is continuously withdrawn. Set up a differential equation that A(t) satisfies, and specify the initial condition on A(t). Do not solve the differential equation. Solving the equation, even if correct, will not receive any ...
Learning Area
... 8.2.5 Solves equations by inspection, trial-and improvement or algebraic processes (additive and multiplicative inverses), checking the solution by substitution. 8.2.9 Interprets and uses the following basic algebraic vocabulary in context: term, expression, coefficient, exponent (or index), base, c ...
... 8.2.5 Solves equations by inspection, trial-and improvement or algebraic processes (additive and multiplicative inverses), checking the solution by substitution. 8.2.9 Interprets and uses the following basic algebraic vocabulary in context: term, expression, coefficient, exponent (or index), base, c ...