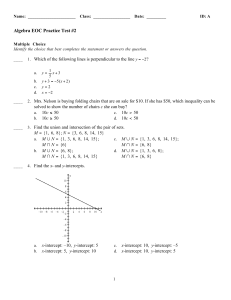
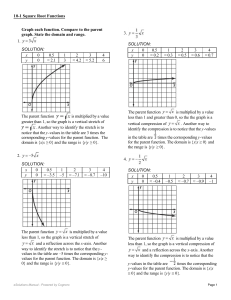
4 Number Theory 1 4.1 Divisors
... Note: This definition satisfies gcd(0,1) = 1. The lowest common multiple lcm(a,b) is defined as follows: lcm(a,b) = min(m > 0 s.t. a|m and b|m) (for a 6= 0 and b 6= 0). a and b are coprimes (or relatively prime) iff gcd(a,b) = 1. Prime Numbers An integer p ≥ 2 is called prime if it is divisible only ...
... Note: This definition satisfies gcd(0,1) = 1. The lowest common multiple lcm(a,b) is defined as follows: lcm(a,b) = min(m > 0 s.t. a|m and b|m) (for a 6= 0 and b 6= 0). a and b are coprimes (or relatively prime) iff gcd(a,b) = 1. Prime Numbers An integer p ≥ 2 is called prime if it is divisible only ...
Notes on Galois Theory
... We shall give an explicit bound for the order of Gal(E/F ) later. Remark 1.10. The homomorphism ρ : Gal(E/F ) → Sn given in Corollary 1.8 depends on a choice of labeling of the roots of f (x) as α1 , . . . , αn . A different choice of labeling the roots corresponds to an element τ ∈ Sn , and it is e ...
... We shall give an explicit bound for the order of Gal(E/F ) later. Remark 1.10. The homomorphism ρ : Gal(E/F ) → Sn given in Corollary 1.8 depends on a choice of labeling of the roots of f (x) as α1 , . . . , αn . A different choice of labeling the roots corresponds to an element τ ∈ Sn , and it is e ...
#1) Simplify and factor: 8x – 4x – 6x + 6 8x-4x-6x+6 Since 8x and
... Since 3 does not contain the variable to solve for, move it to the right-hand side of the equation by subtracting 3 from both sides. -x=-3 ...
... Since 3 does not contain the variable to solve for, move it to the right-hand side of the equation by subtracting 3 from both sides. -x=-3 ...