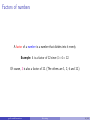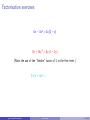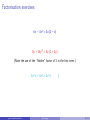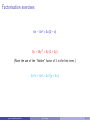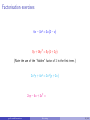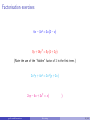Download Factorising - Numeracy Workshop

Please Note
These pdf slides are configured for viewing on a computer screen.
Viewing them on hand-held devices may be difficult as they require a
“slideshow” mode.
Do not try to print them out as there are many more pages than the
number of slides listed at the bottom right of each screen.
Apologies for any inconvenience.
Factorising
Numeracy Workshop
[email protected]
[email protected]
Factorising
2 / 43
Introduction
These slides extend on a basic knowledge of algebra (such as the previous Algebra
workshop Expressions and Expansion). Topics include extracting common factors,
factorising quadratic expressions and polynomials.
[email protected]
Factorising
3 / 43
Introduction
These slides extend on a basic knowledge of algebra (such as the previous Algebra
workshop Expressions and Expansion). Topics include extracting common factors,
factorising quadratic expressions and polynomials.
Workshop resources: These slides are available online:
www.studysmarter.uwa.edu.au → Numeracy and Maths → Online Resources
[email protected]
Factorising
3 / 43
Introduction
These slides extend on a basic knowledge of algebra (such as the previous Algebra
workshop Expressions and Expansion). Topics include extracting common factors,
factorising quadratic expressions and polynomials.
Workshop resources: These slides are available online:
www.studysmarter.uwa.edu.au → Numeracy and Maths → Online Resources
Next Workshop: See your Workshop Calendar →
www.studysmarter.uwa.edu.au
[email protected]
Factorising
3 / 43
Introduction
These slides extend on a basic knowledge of algebra (such as the previous Algebra
workshop Expressions and Expansion). Topics include extracting common factors,
factorising quadratic expressions and polynomials.
Workshop resources: These slides are available online:
www.studysmarter.uwa.edu.au → Numeracy and Maths → Online Resources
Next Workshop: See your Workshop Calendar →
www.studysmarter.uwa.edu.au
Drop-in Study Sessions: Monday, Wednesday, Friday, 10am-12pm, Room 2202,
Second Floor, Social Sciences South Building, every week.
[email protected]
Factorising
3 / 43
Introduction
These slides extend on a basic knowledge of algebra (such as the previous Algebra
workshop Expressions and Expansion). Topics include extracting common factors,
factorising quadratic expressions and polynomials.
Workshop resources: These slides are available online:
www.studysmarter.uwa.edu.au → Numeracy and Maths → Online Resources
Next Workshop: See your Workshop Calendar →
www.studysmarter.uwa.edu.au
Drop-in Study Sessions: Monday, Wednesday, Friday, 10am-12pm, Room 2202,
Second Floor, Social Sciences South Building, every week.
Email: [email protected]
[email protected]
Factorising
3 / 43
Factors of numbers
A factor of a number is a number that divides into it evenly.
[email protected]
Factorising
4 / 43
Factors of numbers
A factor of a number is a number that divides into it evenly.
Example: 4 is a factor of 12 since 3 × 4 = 12.
[email protected]
Factorising
4 / 43
Factors of numbers
A factor of a number is a number that divides into it evenly.
Example: 4 is a factor of 12 since 3 × 4 = 12.
Of course, 3 is also a factor of 12.
[email protected]
Factorising
4 / 43
Factors of numbers
A factor of a number is a number that divides into it evenly.
Example: 4 is a factor of 12 since 3 × 4 = 12.
Of course, 3 is also a factor of 12. (The others are
[email protected]
Factorising
4 / 43
Factors of numbers
A factor of a number is a number that divides into it evenly.
Example: 4 is a factor of 12 since 3 × 4 = 12.
Of course, 3 is also a factor of 12. (The others are 1, 2, 6 and 12.)
[email protected]
Factorising
4 / 43
Factors of terms
A factor of a term is a number, variable or combination that divides into it evenly.
[email protected]
Factorising
5 / 43
Factors of terms
A factor of a term is a number, variable or combination that divides into it evenly.
Example: The term 12x has a factor of 4 since 3x × 4 = 12x.
[email protected]
Factorising
5 / 43
Factors of terms
A factor of a term is a number, variable or combination that divides into it evenly.
Example: The term 12x has a factor of 4 since 3x × 4 = 12x.
Important point: the variable x is also a factor of 12x since 12 × x = 12x. (This
is true even though x could be any number, including non-whole numbers.)
[email protected]
Factorising
5 / 43
Factors of terms
A factor of a term is a number, variable or combination that divides into it evenly.
Example: The term 12x has a factor of 4 since 3x × 4 = 12x.
Important point: the variable x is also a factor of 12x since 12 × x = 12x. (This
is true even though x could be any number, including non-whole numbers.)
Factors of 12x can be made up of combinations of other factors, such as
[email protected]
Factorising
5 / 43
Factors of terms
A factor of a term is a number, variable or combination that divides into it evenly.
Example: The term 12x has a factor of 4 since 3x × 4 = 12x.
Important point: the variable x is also a factor of 12x since 12 × x = 12x. (This
is true even though x could be any number, including non-whole numbers.)
Factors of 12x can be made up of combinations of other factors, such as 2, 6x, 1,
3x, 12, etc.
[email protected]
Factorising
5 / 43
Factors of expressions
In the previous algebra workshop we looked at the expression
4(2x + 3)
[email protected]
Factorising
6 / 43
Factors of expressions
In the previous algebra workshop we looked at the expression
4(2x + 3)
This has two clear factors,
[email protected]
Factorising
6 / 43
Factors of expressions
In the previous algebra workshop we looked at the expression
4(2x + 3)
This has two clear factors, 4 and
[email protected]
Factorising
6 / 43
Factors of expressions
In the previous algebra workshop we looked at the expression
4(2x + 3)
This has two clear factors, 4 and 2x + 3 because
4 × (2x + 3) = 4(2x + 3)
[email protected]
Factorising
6 / 43
Factors of expressions
In the previous algebra workshop we looked at the expression
4(2x + 3)
This has two clear factors, 4 and 2x + 3 because
4 × (2x + 3) = 4(2x + 3)
When we expanded the brackets, we got
4(2x + 3) = 8x + 12
[email protected]
Factorising
6 / 43
Factors of expressions
In the previous algebra workshop we looked at the expression
4(2x + 3)
This has two clear factors, 4 and 2x + 3 because
4 × (2x + 3) = 4(2x + 3)
When we expanded the brackets, we got
4(2x + 3) = 8x + 12
Our task now is to reverse this process.
[email protected]
Factorising
6 / 43
Factors of expressions
In the previous algebra workshop we looked at the expression
4(2x + 3)
This has two clear factors, 4 and 2x + 3 because
4 × (2x + 3) = 4(2x + 3)
When we expanded the brackets, we got
4(2x + 3) = 8x + 12
Our task now is to reverse this process. That is, take an expression like
8x + 12 and extract the factors which are common to both terms (8x and 12).
[email protected]
Factorising
6 / 43
Factors of expressions
In the previous algebra workshop we looked at the expression
4(2x + 3)
This has two clear factors, 4 and 2x + 3 because
4 × (2x + 3) = 4(2x + 3)
When we expanded the brackets, we got
4(2x + 3) = 8x + 12
Our task now is to reverse this process. That is, take an expression like
8x + 12 and extract the factors which are common to both terms (8x and 12).
This process is called factorisation.
[email protected]
Factorising
6 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
[email protected]
Factorising
7 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
What factors do the terms 28x and 98x 2 have in common?
[email protected]
Factorising
7 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
What factors do the terms 28x and 98x 2 have in common?
It might help to imagine some multiplication signs:
28 × x
[email protected]
and
Factorising
98 × x × x
7 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
What factors do the terms 28x and 98x 2 have in common?
It might help to imagine some multiplication signs:
28 × x
and
98 × x × x
So, x is a factor common to both terms.
[email protected]
Factorising
7 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
What factors do the terms 28x and 98x 2 have in common?
It might help to imagine some multiplication signs:
28 × x
and
98 × x × x
So, x is a factor common to both terms. Both numbers are even:
[email protected]
Factorising
7 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
What factors do the terms 28x and 98x 2 have in common?
It might help to imagine some multiplication signs:
28 × x
and
98 × x × x
So, x is a factor common to both terms. Both numbers are even:
2 × 14 × x
[email protected]
and
Factorising
2 × 49 × x × x
7 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
What factors do the terms 28x and 98x 2 have in common?
It might help to imagine some multiplication signs:
28 × x
and
98 × x × x
So, x is a factor common to both terms. Both numbers are even:
2 × 14 × x
and
2 × 49 × x × x
So, 2 is also a common factor.
[email protected]
Factorising
7 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
What factors do the terms 28x and 98x 2 have in common?
It might help to imagine some multiplication signs:
28 × x
and
98 × x × x
So, x is a factor common to both terms. Both numbers are even:
2 × 14 × x
and
2 × 49 × x × x
So, 2 is also a common factor. In fact, this step reveals another one.
[email protected]
Factorising
7 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
What factors do the terms 28x and 98x 2 have in common?
It might help to imagine some multiplication signs:
28 × x
and
98 × x × x
So, x is a factor common to both terms. Both numbers are even:
2 × 14 × x
and
2 × 49 × x × x
So, 2 is also a common factor. In fact, this step reveals another one.
2×2×7×x
[email protected]
and
Factorising
2×7×7×x ×x
7 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
What factors do the terms 28x and 98x 2 have in common?
It might help to imagine some multiplication signs:
28 × x
and
98 × x × x
So, x is a factor common to both terms. Both numbers are even:
2 × 14 × x
and
2 × 49 × x × x
So, 2 is also a common factor. In fact, this step reveals another one.
2×2×7×x
and
2×7×7×x ×x
7 is also a common factor.
[email protected]
Factorising
7 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
2×2×7×x
[email protected]
and
Factorising
2×7×7×x ×x
8 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
2×2×7×x
and
2×7×7×x ×x
The combination of common factors is 2 × 7 × x = 14x.
[email protected]
Factorising
8 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
2×2×7×x
and
2×7×7×x ×x
The combination of common factors is 2 × 7 × x = 14x.
We call this the highest common factor and write it outside some brackets:
[email protected]
Factorising
8 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
2×2×7×x
and
2×7×7×x ×x
The combination of common factors is 2 × 7 × x = 14x.
We call this the highest common factor and write it outside some brackets:
28x + 98x 2 = 14x(
[email protected]
Factorising
)
8 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
2×2×7×x
and
2×7×7×x ×x
The combination of common factors is 2 × 7 × x = 14x.
We call this the highest common factor and write it outside some brackets:
28x + 98x 2 = 14x(
)
The remaining bits of both terms go inside the brackets.
[email protected]
Factorising
8 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
2×2×7×x
and
2×7×7×x ×x
The combination of common factors is 2 × 7 × x = 14x.
We call this the highest common factor and write it outside some brackets:
28x + 98x 2 = 14x(2 + 7x)
The remaining bits of both terms go inside the brackets.
[email protected]
Factorising
8 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
2×2×7×x
and
2×7×7×x ×x
The combination of common factors is 2 × 7 × x = 14x.
We call this the highest common factor and write it outside some brackets:
28x + 98x 2 = 14x(2 + 7x)
The remaining bits of both terms go inside the brackets.
This is the fully factorised form of the original expression.
[email protected]
Factorising
8 / 43
Factorisation example
Example: Factorise 28x + 98x 2 .
2×2×7×x
and
2×7×7×x ×x
The combination of common factors is 2 × 7 × x = 14x.
We call this the highest common factor and write it outside some brackets:
28x + 98x 2 = 14x(2 + 7x)
The remaining bits of both terms go inside the brackets.
This is the fully factorised form of the original expression.
Note: You can check your answer by expanding the factorised form.
[email protected]
Factorising
8 / 43
Factorisation exercises
6x − 3x 2 =
[email protected]
Factorising
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(
[email protected]
Factorising
)
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(2 − x)
[email protected]
Factorising
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(2 − x)
8y + 16y 2 =
[email protected]
Factorising
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(2 − x)
8y + 16y 2 = 8y (
[email protected]
Factorising
)
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(2 − x)
8y + 16y 2 = 8y (1 + 2y )
[email protected]
Factorising
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(2 − x)
8y + 16y 2 = 8y (1 + 2y )
(Note the use of the “hidden” factor of 1 in the first term.)
[email protected]
Factorising
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(2 − x)
8y + 16y 2 = 8y (1 + 2y )
(Note the use of the “hidden” factor of 1 in the first term.)
2x 2 y + 4x 3 =
[email protected]
Factorising
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(2 − x)
8y + 16y 2 = 8y (1 + 2y )
(Note the use of the “hidden” factor of 1 in the first term.)
2x 2 y + 4x 3 = 2x 2 (
[email protected]
Factorising
)
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(2 − x)
8y + 16y 2 = 8y (1 + 2y )
(Note the use of the “hidden” factor of 1 in the first term.)
2x 2 y + 4x 3 = 2x 2 (y + 2x)
[email protected]
Factorising
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(2 − x)
8y + 16y 2 = 8y (1 + 2y )
(Note the use of the “hidden” factor of 1 in the first term.)
2x 2 y + 4x 3 = 2x 2 (y + 2x)
2xy − 4x + 3x 2 =
[email protected]
Factorising
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(2 − x)
8y + 16y 2 = 8y (1 + 2y )
(Note the use of the “hidden” factor of 1 in the first term.)
2x 2 y + 4x 3 = 2x 2 (y + 2x)
2xy − 4x + 3x 2 = x(
[email protected]
Factorising
)
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(2 − x)
8y + 16y 2 = 8y (1 + 2y )
(Note the use of the “hidden” factor of 1 in the first term.)
2x 2 y + 4x 3 = 2x 2 (y + 2x)
2xy − 4x + 3x 2 = x(2y − 4 + 3x)
[email protected]
Factorising
9 / 43
Factorisation exercises
6x − 3x 2 = 3x(2 − x)
8y + 16y 2 = 8y (1 + 2y )
(Note the use of the “hidden” factor of 1 in the first term.)
2x 2 y + 4x 3 = 2x 2 (y + 2x)
2xy − 4x + 3x 2 = x(2y − 4 + 3x)
(Factors must be common to all terms.)
[email protected]
Factorising
9 / 43
Double bracket expressions
Here is a common type of double bracket expression.
(x + 2)(x + 5) =
[email protected]
Factorising
10 / 43
Double bracket expressions
Here is a common type of double bracket expression. Let’s expand the brackets to
see whether there are any useful patterns we can use to reverse the process:
(x + 2)(x + 5) =
[email protected]
Factorising
10 / 43
Double bracket expressions
Here is a common type of double bracket expression. Let’s expand the brackets to
see whether there are any useful patterns we can use to reverse the process:
(x + 2)(x + 5) =
[email protected]
Factorising
10 / 43
Double bracket expressions
Here is a common type of double bracket expression. Let’s expand the brackets to
see whether there are any useful patterns we can use to reverse the process:
(x + 2)(x + 5) = x 2
[email protected]
Factorising
10 / 43
Double bracket expressions
Here is a common type of double bracket expression. Let’s expand the brackets to
see whether there are any useful patterns we can use to reverse the process:
(x + 2)(x + 5) = x 2
[email protected]
Factorising
10 / 43
Double bracket expressions
Here is a common type of double bracket expression. Let’s expand the brackets to
see whether there are any useful patterns we can use to reverse the process:
(x + 2)(x + 5) = x 2 + 5x
[email protected]
Factorising
10 / 43
Double bracket expressions
Here is a common type of double bracket expression. Let’s expand the brackets to
see whether there are any useful patterns we can use to reverse the process:
(x + 2)(x + 5) = x 2 + 5x
[email protected]
Factorising
10 / 43
Double bracket expressions
Here is a common type of double bracket expression. Let’s expand the brackets to
see whether there are any useful patterns we can use to reverse the process:
(x + 2)(x + 5) = x 2 + 5x + 2x
[email protected]
Factorising
10 / 43
Double bracket expressions
Here is a common type of double bracket expression. Let’s expand the brackets to
see whether there are any useful patterns we can use to reverse the process:
(x + 2)(x + 5) = x 2 + 5x + 2x
[email protected]
Factorising
10 / 43
Double bracket expressions
Here is a common type of double bracket expression. Let’s expand the brackets to
see whether there are any useful patterns we can use to reverse the process:
(x + 2)(x + 5) = x 2 + 5x + 2x + 2 × 5
[email protected]
Factorising
10 / 43
Double bracket expressions
Here is a common type of double bracket expression. Let’s expand the brackets to
see whether there are any useful patterns we can use to reverse the process:
(x + 2)(x + 5) = x 2 + 5x + 2x + 2 × 5
= x 2 + (5 + 2)x + 2 × 5
[email protected]
Factorising
10 / 43
Double bracket expressions
Here is a common type of double bracket expression. Let’s expand the brackets to
see whether there are any useful patterns we can use to reverse the process:
(x + 2)(x + 5) = x 2 + 5x + 2x + 2 × 5
= x 2 + (5 + 2)x + 2 × 5
= x2 +
[email protected]
Factorising
7x
+ 10
10 / 43
Double bracket expressions
Here is a common type of double bracket expression. Let’s expand the brackets to
see whether there are any useful patterns we can use to reverse the process:
(x + 2)(x + 5) = x 2 + 5x + 2x + 2 × 5
= x 2 + (5 + 2)x + 2 × 5
= x2 +
7x
+ 10
The pattern is here: 5 + 2 = 7 and 2 × 5 = 10.
[email protected]
Factorising
10 / 43
A Rule
So, in general, whenever we are asked to expand an expression of the form:
(x + a)(x + b)
[email protected]
Factorising
11 / 43
A Rule
So, in general, whenever we are asked to expand an expression of the form:
(x + a)(x + b)
we always end up with
x 2 + (a + b)x + ab
That is, you always add the two numbers a and b together to get the number
multiplying x, and you multiply them to get the constant term.
[email protected]
Factorising
11 / 43
Factorisation
If we are asked to factorise:
x 2 + 5x + 6
then we are being asked to write the above in the form
(x + a)(x + b)
[email protected]
Factorising
12 / 43
Factorisation
If we are asked to factorise:
x 2 + 5x + 6
then we are being asked to write the above in the form
(x + a)(x + b)
where a + b = 5 and a × b = 6. Can you find two numbers which do this?
[email protected]
Factorising
12 / 43
Factorisation
If we are asked to factorise:
x 2 + 5x + 6
then we are being asked to write the above in the form
(x + a)(x + b)
where a + b = 5 and a × b = 6. Can you find two numbers which do this?
The answer is 2 and 3 (2 + 3 = 5, 2 × 3 = 6).
[email protected]
Factorising
12 / 43
Factorisation
If we are asked to factorise:
x 2 + 5x + 6
then we are being asked to write the above in the form
(x + a)(x + b)
where a + b = 5 and a × b = 6. Can you find two numbers which do this?
The answer is 2 and 3 (2 + 3 = 5, 2 × 3 = 6).
So we can factorise the expression as follows:
x 2 + 5x + 6 = (x + 2)(x + 3)
[email protected]
Factorising
12 / 43
Factorisation
Factorise x 2 − 3x − 10
[email protected]
Factorising
13 / 43
Factorisation
Factorise x 2 − 3x − 10
So x 2 − 3x − 10 = (x + a)(x + b)
where a + b = −3 and a × b = −10. Which two numbers do this?
[email protected]
Factorising
13 / 43
Factorisation
Factorise x 2 − 3x − 10
So x 2 − 3x − 10 = (x + a)(x + b)
where a + b = −3 and a × b = −10. Which two numbers do this?
The answer is −5 and 2 (−5 + 2 = −3, −5 × 2 = −10).
[email protected]
Factorising
13 / 43
Factorisation
Factorise x 2 − 3x − 10
So x 2 − 3x − 10 = (x + a)(x + b)
where a + b = −3 and a × b = −10. Which two numbers do this?
The answer is −5 and 2 (−5 + 2 = −3, −5 × 2 = −10).
So we can factorise the expression as follows:
x 2 − 3x − 10 = (x − 5)(x + 2)
[email protected]
Factorising
13 / 43
Removing Factors
We have seen a method which usually works when the multiplier of x 2 is
equal to 1.
What if we were asked to factorise:
3x 2 + 9x + 6
[email protected]
Factorising
14 / 43
Removing Factors
We have seen a method which usually works when the multiplier of x 2 is
equal to 1.
What if we were asked to factorise:
3x 2 + 9x + 6
We notice that the multipliers of all three terms in the above expression are
divisible by 3. Hence, we can factor out this common factor as follows:
3x 2 + 9x + 6 = 3(x 2 + 3x + 2)
[email protected]
Factorising
14 / 43
Removing Factors
We have seen a method which usually works when the multiplier of x 2 is
equal to 1.
What if we were asked to factorise:
3x 2 + 9x + 6
We notice that the multipliers of all three terms in the above expression are
divisible by 3. Hence, we can factor out this common factor as follows:
3x 2 + 9x + 6 = 3(x 2 + 3x + 2)
Now, the expression in brackets is just like we saw on the previous slides, we look
for two numbers which add to 3 and multiply to 2. This gives us:
3x 2 + 9x + 6 = 3
[email protected]
Factorising
14 / 43
Removing Factors
We have seen a method which usually works when the multiplier of x 2 is
equal to 1.
What if we were asked to factorise:
3x 2 + 9x + 6
We notice that the multipliers of all three terms in the above expression are
divisible by 3. Hence, we can factor out this common factor as follows:
3x 2 + 9x + 6 = 3(x 2 + 3x + 2)
Now, the expression in brackets is just like we saw on the previous slides, we look
for two numbers which add to 3 and multiply to 2. This gives us:
3x 2 + 9x + 6 = 3(x + 1)(x + 2)
[email protected]
Factorising
14 / 43
Removing Factors
Factorise the following expression.
5x 2 + 40x + 60
[email protected]
Factorising
15 / 43
Removing Factors
Factorise the following expression.
5x 2 + 40x + 60
Here we see that the multiplier of x 2 is 5. We also notice that all multipliers in
the above expression are divisible by 5. Hence, we can factor out this common
factor as follows:
5x 2 + 40x + 60 = 5(x 2 + 8x + 12)
[email protected]
Factorising
15 / 43
Removing Factors
Factorise the following expression.
5x 2 + 40x + 60
Here we see that the multiplier of x 2 is 5. We also notice that all multipliers in
the above expression are divisible by 5. Hence, we can factor out this common
factor as follows:
5x 2 + 40x + 60 = 5(x 2 + 8x + 12)
Now we look for two numbers which add to 8 and multiply to 12. This gives us:
5x 2 + 40x + 60 = 5
[email protected]
Factorising
15 / 43
Removing Factors
Factorise the following expression.
5x 2 + 40x + 60
Here we see that the multiplier of x 2 is 5. We also notice that all multipliers in
the above expression are divisible by 5. Hence, we can factor out this common
factor as follows:
5x 2 + 40x + 60 = 5(x 2 + 8x + 12)
Now we look for two numbers which add to 8 and multiply to 12. This gives us:
5x 2 + 40x + 60 = 5(x + 2)(x + 6)
[email protected]
Factorising
15 / 43
Factorisation
If we are asked to factorise:
x2 − 9
then we are being asked to write the above in the form
(x + a)(x + b)
[email protected]
Factorising
16 / 43
Factorisation
If we are asked to factorise:
x2 − 9
then we are being asked to write the above in the form
(x + a)(x + b)
It looks different to the expressions we have been factorising because it appears to
have no x term.
[email protected]
Factorising
16 / 43
Factorisation
If we are asked to factorise:
x2 − 9
then we are being asked to write the above in the form
(x + a)(x + b)
It looks different to the expressions we have been factorising because it appears to
have no x term. However, we can make it the same if we include an x term with a
multiplier of
[email protected]
Factorising
16 / 43
Factorisation
If we are asked to factorise:
x2 − 9
then we are being asked to write the above in the form
(x + a)(x + b)
It looks different to the expressions we have been factorising because it appears to
have no x term. However, we can make it the same if we include an x term with a
multiplier of 0:
x 2 +0x − 9
[email protected]
Factorising
16 / 43
Factorisation
If we are asked to factorise:
x2 − 9
then we are being asked to write the above in the form
(x + a)(x + b)
It looks different to the expressions we have been factorising because it appears to
have no x term. However, we can make it the same if we include an x term with a
multiplier of 0:
x 2 +0x − 9
So we know that we need two numbers which add up to 0 and multiply to give
−9. Can you find two numbers which do this?
[email protected]
Factorising
16 / 43
Factorisation
If we are asked to factorise:
x2 − 9
then we are being asked to write the above in the form
(x + a)(x + b)
It looks different to the expressions we have been factorising because it appears to
have no x term. However, we can make it the same if we include an x term with a
multiplier of 0:
x 2 +0x − 9
So we know that we need two numbers which add up to 0 and multiply to give
−9. Can you find two numbers which do this?
The answer is 3 and −3 (3 + −3 = 0, 3 × −3 = −9).
[email protected]
Factorising
16 / 43
Factorisation
If we are asked to factorise:
x2 − 9
then we are being asked to write the above in the form
(x + a)(x + b)
It looks different to the expressions we have been factorising because it appears to
have no x term. However, we can make it the same if we include an x term with a
multiplier of 0:
x 2 +0x − 9
So we know that we need two numbers which add up to 0 and multiply to give
−9. Can you find two numbers which do this?
The answer is 3 and −3 (3 + −3 = 0, 3 × −3 = −9).
So we can factorise the expression as follows:
x 2 − 9 = (x + 3)(x − 3)
[email protected]
Factorising
16 / 43
The Difference of Two Squares
If you are asked to factorise x 2 − 16 we get:
[email protected]
Factorising
17 / 43
The Difference of Two Squares
If you are asked to factorise x 2 − 16 we get:
(x + 4)(x − 4)
[email protected]
Factorising
17 / 43
The Difference of Two Squares
If you are asked to factorise x 2 − 16 we get:
(x + 4)(x − 4)
If you are asked to factorise x 2 − 36 we get:
[email protected]
Factorising
17 / 43
The Difference of Two Squares
If you are asked to factorise x 2 − 16 we get:
(x + 4)(x − 4)
If you are asked to factorise x 2 − 36 we get:
(x + 6)(x − 6)
[email protected]
Factorising
17 / 43
The Difference of Two Squares
If you are asked to factorise x 2 − 16 we get:
(x + 4)(x − 4)
If you are asked to factorise x 2 − 36 we get:
(x + 6)(x − 6)
This leads us to a general formula called the difference of two squares:
x 2 − a2 = (x + a)(x − a)
[email protected]
Factorising
17 / 43
The Difference of Two Squares
If you are asked to factorise x 2 − 16 we get:
(x + 4)(x − 4)
If you are asked to factorise x 2 − 36 we get:
(x + 6)(x − 6)
This leads us to a general formula called the difference of two squares:
x 2 − a2 = (x + a)(x − a)
Tip: Try to avoid memorising too many formulas. It’s handy to remember that
this is just a simple special case of a more general process.
[email protected]
Factorising
17 / 43
The Difference of Two Squares: Examples
x 2 − 25
[email protected]
=
Factorising
18 / 43
The Difference of Two Squares: Examples
x 2 − 25
[email protected]
= (x − 5)(x + 5)
Factorising
18 / 43
The Difference of Two Squares: Examples
[email protected]
x 2 − 25
= (x − 5)(x + 5)
x 2 − 49
=
Factorising
18 / 43
The Difference of Two Squares: Examples
[email protected]
x 2 − 25
= (x − 5)(x + 5)
x 2 − 49
= (x + 7)(x − 7)
Factorising
18 / 43
The Difference of Two Squares: Examples
x 2 − 25
= (x − 5)(x + 5)
x 2 − 49
= (x + 7)(x − 7)
4x 2 − 25
[email protected]
=
Factorising
18 / 43
The Difference of Two Squares: Examples
x 2 − 25
= (x − 5)(x + 5)
x 2 − 49
= (x + 7)(x − 7)
4x 2 − 25
=
(2x)2 − 52
=
[email protected]
Factorising
18 / 43
The Difference of Two Squares: Examples
x 2 − 25
= (x − 5)(x + 5)
x 2 − 49
= (x + 7)(x − 7)
4x 2 − 25
[email protected]
=
(2x)2 − 52
=
(2x − 5)(2x + 5)
Factorising
18 / 43
The Difference of Two Squares: Examples
x 2 − 25
= (x − 5)(x + 5)
x 2 − 49
= (x + 7)(x − 7)
4x 2 − 25
9x 4 − 64
[email protected]
=
(2x)2 − 52
=
(2x − 5)(2x + 5)
=
Factorising
18 / 43
The Difference of Two Squares: Examples
x 2 − 25
= (x − 5)(x + 5)
x 2 − 49
= (x + 7)(x − 7)
4x 2 − 25
9x 4 − 64
=
(2x)2 − 52
=
(2x − 5)(2x + 5)
=
3x 2
2
− 82
=
[email protected]
Factorising
18 / 43
The Difference of Two Squares: Examples
x 2 − 25
= (x − 5)(x + 5)
x 2 − 49
= (x + 7)(x − 7)
4x 2 − 25
9x 4 − 64
=
(2x)2 − 52
=
(2x − 5)(2x + 5)
=
=
[email protected]
3x 2
2
− 82
3x 2 − 8 3x 2 + 8
Factorising
18 / 43
The Difference of Two Squares: Examples
Sometimes we need to factor out the highest common factor:
3x 2 − 75
[email protected]
=
Factorising
19 / 43
The Difference of Two Squares: Examples
Sometimes we need to factor out the highest common factor:
3x 2 − 75
= 3(x 2 − 25)
=
[email protected]
3
Factorising
19 / 43
The Difference of Two Squares: Examples
Sometimes we need to factor out the highest common factor:
3x 2 − 75
= 3(x 2 − 25)
=
[email protected]
3(x + 5)(x − 5)
Factorising
19 / 43
The Difference of Two Squares: Examples
Sometimes we need to factor out the highest common factor:
3x 2 − 75
= 3(x 2 − 25)
=
2x 2 − 8
[email protected]
3(x + 5)(x − 5)
=
Factorising
19 / 43
The Difference of Two Squares: Examples
Sometimes we need to factor out the highest common factor:
3x 2 − 75
2x 2 − 8
[email protected]
= 3(x 2 − 25)
=
3(x + 5)(x − 5)
=
=
2(x 2 − 4)
2
Factorising
19 / 43
The Difference of Two Squares: Examples
Sometimes we need to factor out the highest common factor:
3x 2 − 75
2x 2 − 8
[email protected]
= 3(x 2 − 25)
=
3(x + 5)(x − 5)
=
=
2(x 2 − 4)
2(x + 2)(x − 2)
Factorising
19 / 43
The Difference of Two Squares: Examples
Sometimes we need to factor out the highest common factor:
3x 2 − 75
[email protected]
= 3(x 2 − 25)
=
3(x + 5)(x − 5)
2x 2 − 8
=
=
2(x 2 − 4)
2(x + 2)(x − 2)
x 3 − 25x
=
Factorising
19 / 43
The Difference of Two Squares: Examples
Sometimes we need to factor out the highest common factor:
3x 2 − 75
2x 2 − 8
x 3 − 25x
= 3(x 2 − 25)
=
3(x + 5)(x − 5)
=
=
2(x 2 − 4)
2(x + 2)(x − 2)
= x(x 2 − 25)
= x
[email protected]
Factorising
19 / 43
The Difference of Two Squares: Examples
Sometimes we need to factor out the highest common factor:
3x 2 − 75
2x 2 − 8
x 3 − 25x
= 3(x 2 − 25)
=
3(x + 5)(x − 5)
=
=
2(x 2 − 4)
2(x + 2)(x − 2)
= x(x 2 − 25)
= x(x − 5)(x + 5)
[email protected]
Factorising
19 / 43
The Difference of Two Squares: Examples
Sometimes we need to factor out the highest common factor:
3x 2 − 75
2x 2 − 8
x 3 − 25x
= 3(x 2 − 25)
=
3(x + 5)(x − 5)
=
=
2(x 2 − 4)
2(x + 2)(x − 2)
= x(x 2 − 25)
= x(x − 5)(x + 5)
18x 3 − 32x
[email protected]
=
Factorising
19 / 43
The Difference of Two Squares: Examples
Sometimes we need to factor out the highest common factor:
3x 2 − 75
2x 2 − 8
x 3 − 25x
= 3(x 2 − 25)
=
3(x + 5)(x − 5)
=
=
2(x 2 − 4)
2(x + 2)(x − 2)
= x(x 2 − 25)
= x(x − 5)(x + 5)
18x 3 − 32x
[email protected]
=
=
2x(9x 2 − 16)
2x
Factorising
19 / 43
The Difference of Two Squares: Examples
Sometimes we need to factor out the highest common factor:
3x 2 − 75
2x 2 − 8
x 3 − 25x
= 3(x 2 − 25)
=
3(x + 5)(x − 5)
=
=
2(x 2 − 4)
2(x + 2)(x − 2)
= x(x 2 − 25)
= x(x − 5)(x + 5)
18x 3 − 32x
[email protected]
=
=
2x(9x 2 − 16)
2x(3x + 4)(3x − 4)
Factorising
19 / 43
Harder Factorisation
What if we can’t easily factor out the multiplier of x 2 ?
[email protected]
Factorising
20 / 43
Harder Factorisation
What if we can’t easily factor out the multiplier of x 2 ?
First, consider expanding
(7x + 4)(3x + 5)
[email protected]
Factorising
20 / 43
Harder Factorisation
What if we can’t easily factor out the multiplier of x 2 ?
First, consider expanding
(7x + 4)(3x + 5)
If we do this we get
21x 2 + 35x + 12x + 20
[email protected]
Factorising
20 / 43
Harder Factorisation
What if we can’t easily factor out the multiplier of x 2 ?
First, consider expanding
(7x + 4)(3x + 5)
If we do this we get
21x 2 + 35x + 12x + 20
which then equals
21x 2 + 47x + 20
[email protected]
Factorising
20 / 43
Harder Factorisation
What if we can’t easily factor out the multiplier of x 2 ?
First, consider expanding
(7x + 4)(3x + 5)
If we do this we get
21x 2 + 35x + 12x + 20
which then equals
21x 2 + 47x + 20
Expansion is easy, but doing this problem backwards is tricky if we don’t know
where we started. Our previous methods don’t work here.
[email protected]
Factorising
20 / 43
Harder Factorisation
In general, when we see an expression of the form
Ax 2 + Bx + C
we want to factorise it by writing it in the following form:
(ax + b)(cx + d)
[email protected]
Factorising
21 / 43
Harder Factorisation
In general, when we see an expression of the form
Ax 2 + Bx + C
we want to factorise it by writing it in the following form:
(ax + b)(cx + d)
Note that a and c multiply to ptoduce the multiplier of x 2 (A), and that b and d
multiply to produce the constant on the end (C).
[email protected]
Factorising
21 / 43
Harder Factorisation
In general, when we see an expression of the form
Ax 2 + Bx + C
we want to factorise it by writing it in the following form:
(ax + b)(cx + d)
Note that a and c multiply to ptoduce the multiplier of x 2 (A), and that b and d
multiply to produce the constant on the end (C).
Then we need to play around with it a bit.
[email protected]
Factorising
21 / 43
Harder Factorisation: Example
Factorise 2x 2 + 3x + 1.
[email protected]
Factorising
22 / 43
Harder Factorisation: Example
Factorise 2x 2 + 3x + 1.
We need to write this in the form (ax + b)(cx + d).
[email protected]
Factorising
22 / 43
Harder Factorisation: Example
Factorise 2x 2 + 3x + 1.
We need to write this in the form (ax + b)(cx + d).
The numbers a and c must multiply up to 2, and so one of them must be 1 and
the other must be 2.
[email protected]
Factorising
22 / 43
Harder Factorisation: Example
Factorise 2x 2 + 3x + 1.
We need to write this in the form (ax + b)(cx + d).
The numbers a and c must multiply up to 2, and so one of them must be 1 and
the other must be 2. (It doesn’t matter which is which because multiplication is
commutative.)
(2x + b)(x + d)
[email protected]
Factorising
22 / 43
Harder Factorisation: Example
Factorise 2x 2 + 3x + 1.
We need to write this in the form (ax + b)(cx + d).
The numbers a and c must multiply up to 2, and so one of them must be 1 and
the other must be 2. (It doesn’t matter which is which because multiplication is
commutative.)
(2x + b)(x + d)
The numbers b and d must multiply up to 1, and so one of them must be 1 and
the other must be 1.
(2x + 1)(x + 1)
[email protected]
Factorising
22 / 43
Harder Factorisation: Example
Factorise 7x 2 + 15x + 2.
[email protected]
Factorising
23 / 43
Harder Factorisation: Example
Factorise 7x 2 + 15x + 2.
We need to write this in the form (ax + b)(cx + d).
[email protected]
Factorising
23 / 43
Harder Factorisation: Example
Factorise 7x 2 + 15x + 2.
We need to write this in the form (ax + b)(cx + d).
The numbers a and c must multiply to 7, and so one of them must be 1 and the
other must be 7. It doesn’t matter which is which.
(7x + b)(x + d)
[email protected]
Factorising
23 / 43
Harder Factorisation: Example
Factorise 7x 2 + 15x + 2.
We need to write this in the form (ax + b)(cx + d).
The numbers a and c must multiply to 7, and so one of them must be 1 and the
other must be 7. It doesn’t matter which is which.
(7x + b)(x + d)
The numbers b and d must multiply to 2, so one of them must be 1 and the other
must be 2. The question is, which one is which? There are two possibilities:
(7x + 2)(x + 1)
[email protected]
(7x + 1)(x + 2)
Factorising
23 / 43
Harder Factorisation: Example
Factorise 7x 2 + 15x + 2.
We need to write this in the form (ax + b)(cx + d).
The numbers a and c must multiply to 7, and so one of them must be 1 and the
other must be 7. It doesn’t matter which is which.
(7x + b)(x + d)
The numbers b and d must multiply to 2, so one of them must be 1 and the other
must be 2. The question is, which one is which? There are two possibilities:
(7x + 2)(x + 1)
(7x + 1)(x + 2)
To decide which one is correct, expand them both:
[email protected]
Factorising
23 / 43
Harder Factorisation: Example
Factorise 7x 2 + 15x + 2.
We need to write this in the form (ax + b)(cx + d).
The numbers a and c must multiply to 7, and so one of them must be 1 and the
other must be 7. It doesn’t matter which is which.
(7x + b)(x + d)
The numbers b and d must multiply to 2, so one of them must be 1 and the other
must be 2. The question is, which one is which? There are two possibilities:
(7x + 2)(x + 1)
(7x + 1)(x + 2)
To decide which one is correct, expand them both:
7x 2 + 9x + 2
[email protected]
Factorising
23 / 43
Harder Factorisation: Example
Factorise 7x 2 + 15x + 2.
We need to write this in the form (ax + b)(cx + d).
The numbers a and c must multiply to 7, and so one of them must be 1 and the
other must be 7. It doesn’t matter which is which.
(7x + b)(x + d)
The numbers b and d must multiply to 2, so one of them must be 1 and the other
must be 2. The question is, which one is which? There are two possibilities:
(7x + 2)(x + 1)
(7x + 1)(x + 2)
To decide which one is correct, expand them both:
7x 2 + 9x + 2
[email protected]
7x 2 + 15x + 2
Factorising
23 / 43
Harder Factorisation: Example
Factorise 7x 2 + 15x + 2.
We need to write this in the form (ax + b)(cx + d).
The numbers a and c must multiply to 7, and so one of them must be 1 and the
other must be 7. It doesn’t matter which is which.
(7x + b)(x + d)
The numbers b and d must multiply to 2, so one of them must be 1 and the other
must be 2. The question is, which one is which? There are two possibilities:
(7x + 2)(x + 1)
(7x + 1)(x + 2)
To decide which one is correct, expand them both:
7x 2 + 9x + 2
[email protected]
7x 2 + 15x + 2
Factorising
24 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
[email protected]
Factorising
25 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
[email protected]
Factorising
25 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
The problem now is that both 6 and 10 have multiple possible factorisations!
There are in fact 16 potential answers to test.
[email protected]
Factorising
25 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
The problem now is that both 6 and 10 have multiple possible factorisations!
There are in fact 16 potential answers to test.
The best way to navigate through these options is with a combination of educated
guessing and trial-and-error.
[email protected]
Factorising
25 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
The problem now is that both 6 and 10 have multiple possible factorisations!
There are in fact 16 potential answers to test.
The best way to navigate through these options is with a combination of educated
guessing and trial-and-error. Start by writing out the potential factorisations of 6
and 10 as follows:
[email protected]
Factorising
25 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
The problem now is that both 6 and 10 have multiple possible factorisations!
There are in fact 16 potential answers to test.
The best way to navigate through these options is with a combination of educated
guessing and trial-and-error. Start by writing out the potential factorisations of 6
and 10 as follows:
2
1
2
1
3
6
5
10
6=
[email protected]
Factorising
25 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
The problem now is that both 6 and 10 have multiple possible factorisations!
There are in fact 16 potential answers to test.
The best way to navigate through these options is with a combination of educated
guessing and trial-and-error. Start by writing out the potential factorisations of 6
and 10 as follows:
2
1
2
1
3
6
5
10
In this case, the number term (−10) is negative so we need to get a pair whose
difference is 11.
6=
[email protected]
Factorising
25 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
The problem now is that both 6 and 10 have multiple possible factorisations!
There are in fact 16 potential answers to test.
The best way to navigate through these options is with a combination of educated
guessing and trial-and-error. Start by writing out the potential factorisations of 6
and 10 as follows:
2
1
-2
1
3
6
-5
10
In this case, the number term (−10) is negative so we need to get a pair whose
difference is 11.
1 × 2 = 2 and 6 × 5 = 30. Difference 6= 11. Try again.
[email protected]
Factorising
25 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
The problem now is that both 6 and 10 have multiple possible factorisations!
There are in fact 16 potential answers to test.
The best way to navigate through these options is with a combination of educated
guessing and trial-and-error. Start by writing out the potential factorisations of 6
and 10 as follows:
2
3
1H
*2
HH
HH
j
H
6
5
1
10
In this case, the number term (−10) is negative so we need to get a pair whose
difference is 11.
1 × 5 = 5 and 6 × 2 = 12. Difference 6= 11. Try again.
[email protected]
Factorising
25 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
The problem now is that both 6 and 10 have multiple possible factorisations!
There are in fact 16 potential answers to test.
The best way to navigate through these options is with a combination of educated
guessing and trial-and-error. Start by writing out the potential factorisations of 6
and 10 as follows:
2
1
-2
1
3
6
-5
10
In this case, the number term (−10) is negative so we need to get a pair whose
difference is 11.
2 × 2 = 4 and 3 × 5 = 15. Difference = 11. We have a winner!
[email protected]
Factorising
25 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
We have found that 2 × 2 = 4 and 3 × 5 = 15.
[email protected]
Factorising
26 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
We have found that 2 × 2 = 4 and 3 × 5 = 15.
(2x
[email protected]
5)(3x
Factorising
2)
26 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
We have found that 2 × 2 = 4 and 3 × 5 = 15.
(2x
5)(3x
2)
All we need to do now is place the “+” and “−” signs in the appropriate brackets.
[email protected]
Factorising
26 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
We have found that 2 × 2 = 4 and 3 × 5 = 15.
(2x − 5)(3x + 2)
All we need to do now is place the “+” and “−” signs in the appropriate brackets.
[email protected]
Factorising
26 / 43
Harder Factorisation: Example
Factorise 6x 2 − 11x − 10.
We need to write this in the form (ax + b)(cx + d).
We have found that 2 × 2 = 4 and 3 × 5 = 15.
(2x − 5)(3x + 2)
All we need to do now is place the “+” and “−” signs in the appropriate brackets.
So our answer is
6x 2 − 11x − 10 = (2x − 5)(3x + 2).
[email protected]
Factorising
26 / 43
A final note on double bracket factorisations
Note: Not all expressions of the form ax 2 + bx + c can be factorised into two
brackets easily.
[email protected]
Factorising
27 / 43
A final note on double bracket factorisations
Note: Not all expressions of the form ax 2 + bx + c can be factorised into two
brackets easily. Some can’t be facorised at all. For example
x 2 + 2x + 2
looks easy but cannot be factorised.
[email protected]
Factorising
27 / 43
Why is factorising useful?
Factorising is handy for simplifying expressions and equations, which makes
formulas more efficient to use and problems easier to solve.
[email protected]
Factorising
28 / 43
Why is factorising useful?
Factorising is handy for simplifying expressions and equations, which makes
formulas more efficient to use and problems easier to solve.
Solve for x: x 2 = 6x.
[email protected]
Factorising
28 / 43
Why is factorising useful?
Factorising is handy for simplifying expressions and equations, which makes
formulas more efficient to use and problems easier to solve.
Solve for x: x 2 = 6x.
x 2 − 6x
[email protected]
=
0
(get x terms together)
Factorising
28 / 43
Why is factorising useful?
Factorising is handy for simplifying expressions and equations, which makes
formulas more efficient to use and problems easier to solve.
Solve for x: x 2 = 6x.
[email protected]
x 2 − 6x
=
0
(get x terms together)
x(x − 6)
=
0
(factorise)
Factorising
28 / 43
Why is factorising useful?
Factorising is handy for simplifying expressions and equations, which makes
formulas more efficient to use and problems easier to solve.
Solve for x: x 2 = 6x.
x 2 − 6x
=
0
(get x terms together)
x(x − 6)
=
0
(factorise)
We know that 0 × a = 0, whatever a is, so only one of the two factors above
needs to be 0 to solve the equation:
[email protected]
Factorising
28 / 43
Why is factorising useful?
Factorising is handy for simplifying expressions and equations, which makes
formulas more efficient to use and problems easier to solve.
Solve for x: x 2 = 6x.
x 2 − 6x
=
0
(get x terms together)
x(x − 6)
=
0
(factorise)
We know that 0 × a = 0, whatever a is, so only one of the two factors above
needs to be 0 to solve the equation:
Either
[email protected]
x =0
or
Factorising
x − 6 = 0.
28 / 43
Why is factorising useful?
Factorising is handy for simplifying expressions and equations, which makes
formulas more efficient to use and problems easier to solve.
Solve for x: x 2 = 6x.
x 2 − 6x
=
0
(get x terms together)
x(x − 6)
=
0
(factorise)
We know that 0 × a = 0, whatever a is, so only one of the two factors above
needs to be 0 to solve the equation:
Either
x =0
or
x − 6 = 0.
Hence, the solutions are x = 0 or 6.
[email protected]
Factorising
28 / 43
Why is factorising useful?
Factorising can also simplify algebraic fractions:
[email protected]
Factorising
29 / 43
Why is factorising useful?
Factorising can also simplify algebraic fractions:
4x + 6
2
[email protected]
=
Factorising
29 / 43
Why is factorising useful?
Factorising can also simplify algebraic fractions:
4x + 6
2
[email protected]
=
2(2x + 3)
2
(factorise)
Factorising
29 / 43
Why is factorising useful?
Factorising can also simplify algebraic fractions:
4x + 6
2
=
2(2x + 3)
2
1
=
[email protected]
(factorise)
2(2x + 3)
21
(cancel common factors)
Factorising
29 / 43
Why is factorising useful?
Factorising can also simplify algebraic fractions:
4x + 6
2
=
2(2x + 3)
2
1
=
=
[email protected]
(factorise)
2(2x + 3)
21
(cancel common factors)
2x + 3
Factorising
29 / 43
Why is factorising useful?
Factorising can also simplify algebraic fractions:
[email protected]
Factorising
30 / 43
Why is factorising useful?
Factorising can also simplify algebraic fractions:
x 2 + 3x + 2
x +1
[email protected]
=
Factorising
30 / 43
Why is factorising useful?
Factorising can also simplify algebraic fractions:
x 2 + 3x + 2
x +1
[email protected]
=
(x + 1)(x + 2)
x +1
Factorising
(factorise)
30 / 43
Why is factorising useful?
Factorising can also simplify algebraic fractions:
x 2 + 3x + 2
x +1
=
(x + 1)(x + 2)
x +1
(factorise)
1
=
[email protected]
(x +
1)(x + 2)
x+
11
Factorising
(cancel common factors)
30 / 43
Why is factorising useful?
Factorising can also simplify algebraic fractions:
x 2 + 3x + 2
x +1
=
(x + 1)(x + 2)
x +1
(factorise)
1
=
(x +
1)(x + 2)
x+
11
(cancel common factors)
= x +2
[email protected]
Factorising
30 / 43
Why is factorising useful?
Factorising can also simplify algebraic fractions:
x 2 + 3x + 2
x +1
=
(x + 1)(x + 2)
x +1
(factorise)
1
=
(x +
1)(x + 2)
x+
11
(cancel common factors)
= x +2
Note: Watch out when you cancel terms involving variables. The original fraction
makes it clear that there is a problem when x = −1 because the fraction becomes
0
0 , which is an indeterminate quantity. This problem is no longer obvious in the
simplified version. Usually, we would write the answer as
x + 2,
[email protected]
x 6= −1
Factorising
30 / 43
Polynomials
This final section is about polynomials, a topic which may not be on your maths
syllabus.
[email protected]
Factorising
31 / 43
Polynomials
[email protected]
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
[email protected]
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
[email protected]
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
3x 2 − 6x + 7x 5 + 2
[email protected]
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
3x 2 − 6x + 7x 5 + 2
Look at the above polynomial. Every term in it is either a positive integer power
of the variable x or a constant term.
[email protected]
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
3x 2 − 6x + 7x 5 + 2
Look at the above polynomial. Every term in it is either a positive integer power
of the variable x or a constant term.
Term
3x
[email protected]
Power of x
2
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
3x 2 − 6x + 7x 5 + 2
Look at the above polynomial. Every term in it is either a positive integer power
of the variable x or a constant term.
Term
3x
[email protected]
Power of x
2
2
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
3x 2 − 6x + 7x 5 + 2
Look at the above polynomial. Every term in it is either a positive integer power
of the variable x or a constant term.
Term
Power of x
2
2
3x
7x 5
[email protected]
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
3x 2 − 6x + 7x 5 + 2
Look at the above polynomial. Every term in it is either a positive integer power
of the variable x or a constant term.
Term
Power of x
2
2
5
3x
7x 5
[email protected]
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
3x 2 − 6x + 7x 5 + 2
Look at the above polynomial. Every term in it is either a positive integer power
of the variable x or a constant term.
Term
Power of x
2
2
5
3x
7x 5
−6x
[email protected]
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
3x 2 − 6x + 7x 5 + 2
Look at the above polynomial. Every term in it is either a positive integer power
of the variable x or a constant term.
Term
Power of x
2
2
5
1
3x
7x 5
−6x
[email protected]
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
3x 2 − 6x + 7x 5 + 2
Look at the above polynomial. Every term in it is either a positive integer power
of the variable x or a constant term.
Term
Power of x
2
2
5
1
3x
7x 5
−6x
2
[email protected]
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
3x 2 − 6x + 7x 5 + 2
Look at the above polynomial. Every term in it is either a positive integer power
of the variable x or a constant term.
Term
2
3x
7x 5
−6x
2
[email protected]
Power of x
2
5
1
constant term
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
3x 2 − 6x + 7x 5 + 2
Look at the above polynomial. Every term in it is either a positive integer power
of the variable x or a constant term.
Term
2
3x
7x 5
−6x
2
[email protected]
Power of x
2
5
1
constant term or “2x 0 ”
Factorising
32 / 43
Polynomials
A polynomial is a bunch of terms involving whole number powers (ie. positive
integers) of a variable added/subtracted together.
We might also have a constant term (a single number) as well.
3x 2 − 6x + 7x 5 + 2
Look at the above polynomial. Every term in it is either a positive integer power
of the variable x or a constant term.
Term
2
3x
7x 5
−6x
2
[email protected]
Power of x
2
5
1
constant term or “2x 0 ”
(so the power of x is 0)
Factorising
32 / 43
Polynomials: Examples
7p 8 − 62p 2 + 5 − p 3
[email protected]
Factorising
33 / 43
Polynomials: Examples
7p 8 − 62p 2 + 5 − p 3
7y 2 − 3y 4
[email protected]
Factorising
33 / 43
Polynomials: Examples
7p 8 − 62p 2 + 5 − p 3
7y 2 − 3y 4
3+x
[email protected]
Factorising
33 / 43
Polynomials: Examples
7p 8 − 62p 2 + 5 − p 3
7y 2 − 3y 4
3+x
2 5
3q
+ q 4 + 3q 7 − 2q + 1
(Note that the numbers multiplying the variable parts do not have to be whole
numbers.)
[email protected]
Factorising
33 / 43
Polynomials: A Convention
Polynomials are usually written with their powers in descending order.
7p 8 − 62p 2 + 5 − p 3
[email protected]
Factorising
34 / 43
Polynomials: A Convention
Polynomials are usually written with their powers in descending order.
7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5
[email protected]
Factorising
34 / 43
Polynomials: A Convention
Polynomials are usually written with their powers in descending order.
7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5
7y 2 − 3y 4
[email protected]
Factorising
34 / 43
Polynomials: A Convention
Polynomials are usually written with their powers in descending order.
7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5
7y 2 − 3y 4 −→ −3y 4 + 7y 2
[email protected]
Factorising
34 / 43
Polynomials: A Convention
Polynomials are usually written with their powers in descending order.
7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5
7y 2 − 3y 4 −→ −3y 4 + 7y 2
3+x
[email protected]
Factorising
34 / 43
Polynomials: A Convention
Polynomials are usually written with their powers in descending order.
7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5
7y 2 − 3y 4 −→ −3y 4 + 7y 2
3 + x −→ x + 3
[email protected]
Factorising
34 / 43
Polynomials: A Convention
Polynomials are usually written with their powers in descending order.
7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5
7y 2 − 3y 4 −→ −3y 4 + 7y 2
3 + x −→ x + 3
2 5
3q
+ q 4 + 3q 7 − 2q + 1
[email protected]
Factorising
34 / 43
Polynomials: A Convention
Polynomials are usually written with their powers in descending order.
7p 8 − 62p 2 + 5 − p 3 −→ 7p 8 − p 3 − 62p 2 + 5
7y 2 − 3y 4 −→ −3y 4 + 7y 2
3 + x −→ x + 3
2 5
3q
+ q 4 + 3q 7 − 2q + 1 −→ 3q 7 + 32 q 5 + q 4 − 2q + 1
[email protected]
Factorising
34 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is 7.
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is 7.
The coefficient of x 7 is 3.
(The number multiplying the x part.)
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is 7.
The coefficient of x 7 is 3.
(The number multiplying the x part.)
The coefficient of x 5 is
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is 7.
The coefficient of x 7 is 3.
(The number multiplying the x part.)
The coefficient of x 5 is −4.
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is 7.
The coefficient of x 7 is 3.
(The number multiplying the x part.)
The coefficient of x 5 is −4.
The coefficient of x 4 is
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is 7.
The coefficient of x 7 is 3.
(The number multiplying the x part.)
The coefficient of x 5 is −4.
The coefficient of x 4 is 37 .
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is 7.
The coefficient of x 7 is 3.
(The number multiplying the x part.)
The coefficient of x 5 is −4.
The coefficient of x 4 is 37 .
The coefficient of x is
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is 7.
The coefficient of x 7 is 3.
(The number multiplying the x part.)
The coefficient of x 5 is −4.
The coefficient of x 4 is 37 .
The coefficient of x is −2.
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is 7.
The coefficient of x 7 is 3.
(The number multiplying the x part.)
The coefficient of x 5 is −4.
The coefficient of x 4 is 37 .
The coefficient of x is −2.
The coefficient of x 0 is
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is 7.
The coefficient of x 7 is 3.
(The number multiplying the x part.)
The coefficient of x 5 is −4.
The coefficient of x 4 is 37 .
The coefficient of x is −2.
The coefficient of x 0 is 9 (constant term).
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is 7.
The coefficient of x 7 is 3.
(The number multiplying the x part.)
The coefficient of x 5 is −4.
The coefficient of x 4 is 37 .
The coefficient of x is −2.
The coefficient of x 0 is 9 (constant term).
The coefficient of x 2 is
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
3x 7 − 4x 5 + 37 x 4 − 2x + 9
We say it is a “polynomial in the variable x”.
The order of a polynomial is the highest power of x present. In this case, the
order is 7.
The coefficient of x 7 is 3.
(The number multiplying the x part.)
The coefficient of x 5 is −4.
The coefficient of x 4 is 37 .
The coefficient of x is −2.
The coefficient of x 0 is 9 (constant term).
The coefficient of x 2 is 0 (because it isn’t there!).
[email protected]
Factorising
35 / 43
Polynomials: Terminology
Consider the following polynomial.
4x 3 − 5x − 9
What is the order of this polynomial?
[email protected]
Factorising
36 / 43
Polynomials: Terminology
Consider the following polynomial.
4x 3 − 5x − 9
What is the order of this polynomial? 3
[email protected]
Factorising
36 / 43
Polynomials: Terminology
Consider the following polynomial.
4x 3 − 5x − 9
What is the order of this polynomial? 3
What is the coefficient of x 3 ?
[email protected]
Factorising
36 / 43
Polynomials: Terminology
Consider the following polynomial.
4x 3 − 5x − 9
What is the order of this polynomial? 3
What is the coefficient of x 3 ? 4
[email protected]
Factorising
36 / 43
Polynomials: Terminology
Consider the following polynomial.
4x 3 − 5x − 9
What is the order of this polynomial? 3
What is the coefficient of x 3 ? 4
What is the coefficient of x 2 ?
[email protected]
Factorising
36 / 43
Polynomials: Terminology
Consider the following polynomial.
4x 3 − 5x − 9
What is the order of this polynomial? 3
What is the coefficient of x 3 ? 4
What is the coefficient of x 2 ? 0
[email protected]
Factorising
36 / 43
Polynomials: Terminology
Consider the following polynomial.
4x 3 − 5x − 9
What is the order of this polynomial? 3
What is the coefficient of x 3 ? 4
What is the coefficient of x 2 ? 0
What is the coefficient of x?
[email protected]
Factorising
36 / 43
Polynomials: Terminology
Consider the following polynomial.
4x 3 − 5x − 9
What is the order of this polynomial? 3
What is the coefficient of x 3 ? 4
What is the coefficient of x 2 ? 0
What is the coefficient of x? −5
[email protected]
Factorising
36 / 43
Polynomials: Terminology
Consider the following polynomial.
4x 3 − 5x − 9
What is the order of this polynomial? 3
What is the coefficient of x 3 ? 4
What is the coefficient of x 2 ? 0
What is the coefficient of x? −5
What is the coeficient of x 0 ?
[email protected]
Factorising
36 / 43
Polynomials: Terminology
Consider the following polynomial.
4x 3 − 5x − 9
What is the order of this polynomial? 3
What is the coefficient of x 3 ? 4
What is the coefficient of x 2 ? 0
What is the coefficient of x? −5
What is the coeficient of x 0 ? −9
[email protected]
Factorising
36 / 43
Importance
Why are polynomial expressions important?
[email protected]
Factorising
37 / 43
Importance
Why are polynomial expressions important?
They are easier to work with than other expressions (hard to know this unless you
have worked with other expressions).
[email protected]
Factorising
37 / 43
Importance
Why are polynomial expressions important?
They are easier to work with than other expressions (hard to know this unless you
have worked with other expressions).
Most other expressions can be very closely approximated by polynomial
expressions.
[email protected]
Factorising
37 / 43
Importance
Why are polynomial expressions important?
They are easier to work with than other expressions (hard to know this unless you
have worked with other expressions).
Most other expressions can be very closely approximated by polynomial
expressions.
In a sense, polynomial expressions are mathematical “building blocks”.
[email protected]
Factorising
37 / 43
Adding and Subtracting Polynomials
When we add or subtract polynomials we get a new polynomial (just like we do
with numbers!). This can be done by adding and subtracting their like terms.
(4x 2 + 3x + 7) + (2x 2 + 5x + 2)
[email protected]
Factorising
38 / 43
Adding and Subtracting Polynomials
When we add or subtract polynomials we get a new polynomial (just like we do
with numbers!). This can be done by adding and subtracting their like terms.
(4x 2 + 3x + 7) + (2x 2 + 5x + 2)
We may drop the brackets in this case (why?).
4x 2 + 3x + 7 + 2x 2 + 5x + 2
[email protected]
Factorising
38 / 43
Adding and Subtracting Polynomials
When we add or subtract polynomials we get a new polynomial (just like we do
with numbers!). This can be done by adding and subtracting their like terms.
(4x 2 + 3x + 7) + (2x 2 + 5x + 2)
We may drop the brackets in this case (why?).
4x 2 + 3x + 7 + 2x 2 + 5x + 2
If you need to, shift the signed terms around so that like terms are next to each
other.
4x 2 + 2x 2 + 3x + 5x + 7 + 2
[email protected]
Factorising
38 / 43
Adding and Subtracting Polynomials
When we add or subtract polynomials we get a new polynomial (just like we do
with numbers!). This can be done by adding and subtracting their like terms.
(4x 2 + 3x + 7) + (2x 2 + 5x + 2)
We may drop the brackets in this case (why?).
4x 2 + 3x + 7 + 2x 2 + 5x + 2
If you need to, shift the signed terms around so that like terms are next to each
other.
4x 2 + 2x 2 + 3x + 5x + 7 + 2
We now add like terms together.
6x 2 + 8x + 9
[email protected]
Factorising
38 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
= 3x 3 − 4x 2 + 5
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
= 3x 3 − 4x 2 + 5
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
= 3x 3 − 4x 2 + 5 − x 3
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
= 3x 3 − 4x 2 + 5 − x 3
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
= 3x 3 − 4x 2 + 5 − x 3 − 3x
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
= 3x 3 − 4x 2 + 5 − x 3 − 3x
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
= 3x 3 − 4x 2 + 5 − x 3 − 3x + 4
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
= 3x 3 − 4x 2 + 5 − x 3 − 3x + 4
(In short, every sign in the 2nd bracket changes.)
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
= 3x 3 − 4x 2 + 5 − x 3 − 3x + 4
(In short, every sign in the 2nd bracket changes.)
If you need to, shift the signed terms around so that like terms are next to each
other.
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
= 3x 3 − 4x 2 + 5 − x 3 − 3x + 4
(In short, every sign in the 2nd bracket changes.)
If you need to, shift the signed terms around so that like terms are next to each
other.
3
3
3x − x − 4x 2 − 3x + 5 + 4
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
= 3x 3 − 4x 2 + 5 − x 3 − 3x + 4
(In short, every sign in the 2nd bracket changes.)
If you need to, shift the signed terms around so that like terms are next to each
other.
3
3
3x − x − 4x 2 − 3x + 5 + 4
We now add like terms together.
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
(3x − 4x 2 + 5) − (x 3 + 3x − 4)
3
There is a negative sign to the left of the second set of brackets. This is
effectively a multiplier of −1. From the previous workshop, we know that this −1
gets distributed to each term in the bracket.
3x 3 − 4x 2 + 5 − (x 3 + 3x − 4)
= 3x 3 − 4x 2 + 5 − x 3 − 3x + 4
(In short, every sign in the 2nd bracket changes.)
If you need to, shift the signed terms around so that like terms are next to each
other.
3
3
3x − x − 4x 2 − 3x + 5 + 4
We now add like terms together.
2x 3 − 4x 2 − 3x + 9
[email protected]
Factorising
39 / 43
Adding and Subtracting Polynomials
Simplify the following:
4
−2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
[email protected]
Factorising
40 / 43
Adding and Subtracting Polynomials
Simplify the following:
4
−2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
Once again, the number out the front of each brackets gets distributed to each of
the terms.
−2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
[email protected]
Factorising
40 / 43
Adding and Subtracting Polynomials
Simplify the following:
4
−2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
Once again, the number out the front of each brackets gets distributed to each of
the terms.
−2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
= −12x 4
[email protected]
Factorising
40 / 43
Adding and Subtracting Polynomials
Simplify the following:
4
−2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
Once again, the number out the front of each brackets gets distributed to each of
the terms.
−2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
= −12x 4 + 14x 2
[email protected]
Factorising
40 / 43
Adding and Subtracting Polynomials
Simplify the following:
4
−2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
Once again, the number out the front of each brackets gets distributed to each of
the terms.
−2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
= −12x 4 + 14x 2 + 6
[email protected]
Factorising
40 / 43
Adding and Subtracting Polynomials
Simplify the following:
4
−2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
Once again, the number out the front of each brackets gets distributed to each of
the terms.
−2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
= −12x 4 + 14x 2 + 6 − 40x 6
[email protected]
Factorising
40 / 43
Adding and Subtracting Polynomials
Simplify the following:
4
−2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
Once again, the number out the front of each brackets gets distributed to each of
the terms.
−2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
= −12x 4 + 14x 2 + 6 − 40x 6 + 15x 4
[email protected]
Factorising
40 / 43
Adding and Subtracting Polynomials
Simplify the following:
4
−2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
Once again, the number out the front of each brackets gets distributed to each of
the terms.
−2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
= −12x 4 + 14x 2 + 6 − 40x 6 + 15x 4 − 20
[email protected]
Factorising
40 / 43
Adding and Subtracting Polynomials
Simplify the following:
4
−2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
Once again, the number out the front of each brackets gets distributed to each of
the terms.
−2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
= −12x 4 + 14x 2 + 6 − 40x 6 + 15x 4 − 20
If you need to, shift the signed terms around so that like terms are next to each
other.
−12x 4 + 15x 4 + 14x 2 + 6 − 20 − 40x 6
[email protected]
Factorising
40 / 43
Adding and Subtracting Polynomials
Simplify the following:
4
−2(6x − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
Once again, the number out the front of each brackets gets distributed to each of
the terms.
−2(6x 4 − 7x 2 − 3) + 5(−8x 6 + 3x 4 − 4)
= −12x 4 + 14x 2 + 6 − 40x 6 + 15x 4 − 20
If you need to, shift the signed terms around so that like terms are next to each
other.
−12x 4 + 15x 4 + 14x 2 + 6 − 20 − 40x 6
We now add like terms together and write with decreasing powers:
−40x 6 + 3x 4 + 14x 2 − 14
[email protected]
Factorising
40 / 43
Multiplying Polynomials
We can use the distributive law to multiply two polynomials together
(3x 2 + 2x)(4x 5 + 3x) =
[email protected]
Factorising
41 / 43
Multiplying Polynomials
We can use the distributive law to multiply two polynomials together
(3x 2 + 2x)(4x 5 + 3x) =
[email protected]
Factorising
41 / 43
Multiplying Polynomials
We can use the distributive law to multiply two polynomials together
(3x 2 + 2x)(4x 5 + 3x) = 12x 7
[email protected]
Factorising
41 / 43
Multiplying Polynomials
We can use the distributive law to multiply two polynomials together
(3x 2 + 2x)(4x 5 + 3x) = 12x 7
[email protected]
Factorising
41 / 43
Multiplying Polynomials
We can use the distributive law to multiply two polynomials together
(3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3
[email protected]
Factorising
41 / 43
Multiplying Polynomials
We can use the distributive law to multiply two polynomials together
(3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3
[email protected]
Factorising
41 / 43
Multiplying Polynomials
We can use the distributive law to multiply two polynomials together
(3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3+ 8x 6
[email protected]
Factorising
41 / 43
Multiplying Polynomials
We can use the distributive law to multiply two polynomials together
(3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3+ 8x 6
[email protected]
Factorising
41 / 43
Multiplying Polynomials
We can use the distributive law to multiply two polynomials together
(3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3+ 8x 6+ 6x 2
[email protected]
Factorising
41 / 43
Multiplying Polynomials
We can use the distributive law to multiply two polynomials together
(3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3+ 8x 6+ 6x 2
Every term in the first bracket meets every term in the second bracket.
(We saw this in the previous workshop.)
[email protected]
Factorising
41 / 43
Multiplying Polynomials
We can use the distributive law to multiply two polynomials together
(3x 2 + 2x)(4x 5 + 3x) = 12x 7 + 9x 3+ 8x 6+ 6x 2
Every term in the first bracket meets every term in the second bracket.
(We saw this in the previous workshop.)
Sometimes, we work with “longer” polynomials. The rule is still the same. Every
term in the first bracket must meet every term in the second bracket.
[email protected]
Factorising
41 / 43
Expansion
In general
(polynomial) × (polynomial)
[email protected]
Factorising
42 / 43
Expansion
In general
(polynomial) × (polynomial)
expands out to
polynomial
[email protected]
Factorising
42 / 43
Expansion
In general
(polynomial) × (polynomial)
expands out to
polynomial
Note: We saw earlier that 2nd order polynomials can (sometimes) be factorised.
[email protected]
Factorising
42 / 43
Expansion
In general
(polynomial) × (polynomial)
expands out to
polynomial
Note: We saw earlier that 2nd order polynomials can (sometimes) be factorised.
In general, polynomials can also (sometimes) be be factorised.
[email protected]
Factorising
42 / 43
Expansion
In general
(polynomial) × (polynomial)
expands out to
polynomial
Note: We saw earlier that 2nd order polynomials can (sometimes) be factorised.
In general, polynomials can also (sometimes) be be factorised.
However, that’s a topic for another time . . .
[email protected]
Factorising
42 / 43
Using STUDYSmarter Resources
This resource was developed for UWA students by the STUDYSmarter team for
the numeracy program. When using our resources, please retain them in their
original form with both the STUDYSmarter heading and the UWA crest.
[email protected]
Factorising
43 / 43