DOC - JMap
... 7 In a certain high school, a survey revealed the mean amount of bottled water consumed by students each day was 153 bottles with a standard deviation of 22 bottles. Assuming the survey represented a normal distribution, what is the range of the number of bottled waters that approximately 68.2% of t ...
... 7 In a certain high school, a survey revealed the mean amount of bottled water consumed by students each day was 153 bottles with a standard deviation of 22 bottles. Assuming the survey represented a normal distribution, what is the range of the number of bottled waters that approximately 68.2% of t ...
the arithmetical theory of linear recurring series
... is self-explanatory. The following convenient definition was introduced by H. T. Engstrom*: A number ir is said to be a general period of the difference equation (1.1) for the modulus m if every sequence of rational integers (m) satisfying (1.1) has the period ir. Let t be the least such general per ...
... is self-explanatory. The following convenient definition was introduced by H. T. Engstrom*: A number ir is said to be a general period of the difference equation (1.1) for the modulus m if every sequence of rational integers (m) satisfying (1.1) has the period ir. Let t be the least such general per ...
Chapter 2 Review Key
... feet when it is a horizontal distance of 18 feet from the player. Write a function to represent the height of the ball in terms of its distance from the player. 6. Jeremy stands on the edge of a river and throws a rock into the water. The rock leaves his hand at a height 5 feet above the water. It m ...
... feet when it is a horizontal distance of 18 feet from the player. Write a function to represent the height of the ball in terms of its distance from the player. 6. Jeremy stands on the edge of a river and throws a rock into the water. The rock leaves his hand at a height 5 feet above the water. It m ...
Boole`s Algebra Isn`t Boolean Algebra (Article Review)
... The paper begins with some insightful observations on the state of algebra in Boole’s day as compared with later developments. Noting that Boolean algebra is of much later vintage than Boole’s work, the paper goes on to the stronger suggestion that the underlying ideas for Boole’s work are not those ...
... The paper begins with some insightful observations on the state of algebra in Boole’s day as compared with later developments. Noting that Boolean algebra is of much later vintage than Boole’s work, the paper goes on to the stronger suggestion that the underlying ideas for Boole’s work are not those ...
Polynomials in the Nation`s Service: Using Algebra to Design the
... holds the decryption key, is an excellent demonstration of this. Both Diffie-Hellman key exchange and the RSA encryption algorithm rely on elementary number theory, while elliptic curves power more advanced public-key systems [21], [4]. But while public key has captured mathematicians’ attention, su ...
... holds the decryption key, is an excellent demonstration of this. Both Diffie-Hellman key exchange and the RSA encryption algorithm rely on elementary number theory, while elliptic curves power more advanced public-key systems [21], [4]. But while public key has captured mathematicians’ attention, su ...
1 - JustAnswer
... length of a side of the original square. The length of a side of the original square is 6 cm. 26. Multiply and simplify. Assume variables represent nonzero real numbers. c16 c 0 = c 16 (Simplify your answer. Type exponential notation with positive exponents.) 27. Jack usually mows his lawn in 4 ho ...
... length of a side of the original square. The length of a side of the original square is 6 cm. 26. Multiply and simplify. Assume variables represent nonzero real numbers. c16 c 0 = c 16 (Simplify your answer. Type exponential notation with positive exponents.) 27. Jack usually mows his lawn in 4 ho ...
ARITHMETIC PROGRESSIONS OF THREE SQUARES 1
... correspond to what we’re really interested in (which are the solutions [r, s, t, 1]), but we will make use of them in a geometric construction in projective space. Each equation in (A.1) defines a surface in P3 (R), so we anticipate that the common solution set to both equations is a curve in P3 (R) ...
... correspond to what we’re really interested in (which are the solutions [r, s, t, 1]), but we will make use of them in a geometric construction in projective space. Each equation in (A.1) defines a surface in P3 (R), so we anticipate that the common solution set to both equations is a curve in P3 (R) ...
COMPLEX CURVE SINGULARITIES: A BIASED INTRODUCTION
... we shall consider only polynomials or convergent power series. In this case the functions zi (t) may be defined only in a neighborhood of some point, which we will usually assume to be the origin t = 0 and it is convenient to assume that zi (0) = 0 for all i; one may reduce to this case by a transla ...
... we shall consider only polynomials or convergent power series. In this case the functions zi (t) may be defined only in a neighborhood of some point, which we will usually assume to be the origin t = 0 and it is convenient to assume that zi (0) = 0 for all i; one may reduce to this case by a transla ...
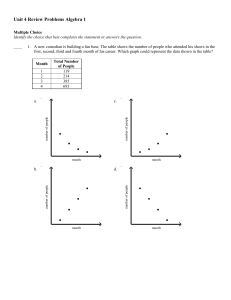
Unit 4 Review Problems Algebra 1 Answer Section
... ____ 30. The grocery store sells dates for $4.00 a pound and pomegranates for $2.75 a pound. Write an equation in standard form for the weights of dates d and pomegranates p that a customer could buy with $12. a. 4p + 2.75d = 12 c. 4d + 2.75p = 12 b. 4d = 2.75p + 12 d. 4 + 2.75 = d Write an equation ...
... ____ 30. The grocery store sells dates for $4.00 a pound and pomegranates for $2.75 a pound. Write an equation in standard form for the weights of dates d and pomegranates p that a customer could buy with $12. a. 4p + 2.75d = 12 c. 4d + 2.75p = 12 b. 4d = 2.75p + 12 d. 4 + 2.75 = d Write an equation ...
Equation

In mathematics, an equation is an equality containing one or more variables. Solving the equation consists of determining which values of the variables make the equality true. In this situation, variables are also known as unknowns and the values which satisfy the equality are known as solutions. An equation differs from an identity in that an equation is not necessarily true for all possible values of the variable.There are many types of equations, and they are found in all areas of mathematics; the techniques used to examine them differ according to their type.Algebra studies two main families of equations: polynomial equations and, among them, linear equations. Polynomial equations have the form P(X) = 0, where P is a polynomial. Linear equations have the form a(x) + b = 0, where a is a linear function and b is a vector. To solve them, one uses algorithmic or geometric techniques, coming from linear algebra or mathematical analysis. Changing the domain of a function can change the problem considerably. Algebra also studies Diophantine equations where the coefficients and solutions are integers. The techniques used are different and come from number theory. These equations are difficult in general; one often searches just to find the existence or absence of a solution, and, if they exist, to count the number of solutions.Geometry uses equations to describe geometric figures. The objective is now different, as equations are used to describe geometric properties. In this context, there are two large families of equations, Cartesian equations and parametric equations.Differential equations are equations involving one or more functions and their derivatives. They are solved by finding an expression for the function that does not involve derivatives. Differential equations are used to model real-life processes in areas such as physics, chemistry, biology, and economics.The ""="" symbol was invented by Robert Recorde (1510–1558), who considered that nothing could be more equal than parallel straight lines with the same length.












![arXiv:math/0007066v1 [math.DG] 11 Jul 2000](http://s1.studyres.com/store/data/015084201_1-90e03a23823ffee28410b900d59e5167-300x300.png)