Solving and Graphing Linear Equations in Two Variables
... Solving and Graphing Linear Equations in Two Variables-Answer Key Across ...
... Solving and Graphing Linear Equations in Two Variables-Answer Key Across ...
Chapters 7 and 8 Slides
... • The graph of the quadratic function defined by f(x) = a(x-h)2 + k, a not 0, is a parabola with vertex (h,k) and the vertical line x = h as axis of symmetry • The graph opens up if a is positive and down if a is negative • The graph is wide if |a|<1 and narrow if |a|>1 compared to y = x2 ...
... • The graph of the quadratic function defined by f(x) = a(x-h)2 + k, a not 0, is a parabola with vertex (h,k) and the vertical line x = h as axis of symmetry • The graph opens up if a is positive and down if a is negative • The graph is wide if |a|<1 and narrow if |a|>1 compared to y = x2 ...
Lesson 32 - Math @ Purdue
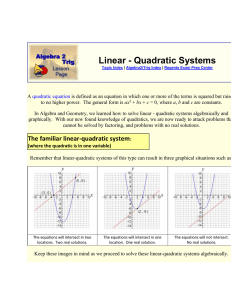
... A linear equation with two variables has infinite solutions (many ordered pairs, example 2 x 3 y 6 ) However, if a second equation is also considered, and we want to know what ordered pairs they may have in common, how many solutions may there be? When two linear equations are considered togethe ...
... A linear equation with two variables has infinite solutions (many ordered pairs, example 2 x 3 y 6 ) However, if a second equation is also considered, and we want to know what ordered pairs they may have in common, how many solutions may there be? When two linear equations are considered togethe ...
a2_c01_l6 - Ms Wood
... If a = b, then ac = bc. a c If a = b, then = , b d where c 0. Copyright © by Holt, Rinehart and Winston. All Rights Reserved. ...
... If a = b, then ac = bc. a c If a = b, then = , b d where c 0. Copyright © by Holt, Rinehart and Winston. All Rights Reserved. ...
MATH 4512. Differential Equations with Applications. Problems and Solutions
... Therefore, the general solution to the given equation is y = µ−1 · (−x−3 + C) = −x−1 + Cx2 . Note that the constant C may be different on the sets {x > 0} and {x < 0}. The initial condition y(1) = 0 belongs to the set {x > 0}. In this set, we must have C = 1, and finally, y(x) = x2 − x−1 ...
... Therefore, the general solution to the given equation is y = µ−1 · (−x−3 + C) = −x−1 + Cx2 . Note that the constant C may be different on the sets {x > 0} and {x < 0}. The initial condition y(1) = 0 belongs to the set {x > 0}. In this set, we must have C = 1, and finally, y(x) = x2 − x−1 ...
Radical Equations SN
... e.g. 3) We have seen that the period of a pendulum, T seconds, is related to the length of the ...
... e.g. 3) We have seen that the period of a pendulum, T seconds, is related to the length of the ...
General history of algebra
... Indian and Arabic Mathematics • India took Greek mathematics and developed early symbolic methods • Arab mathematicians extended and spread Indian algebra to Europe • The word "algebra" is named after the Arabic word "al-jabr" from the title of Persian mathematician Muhammad ibn Mūsā alkhwārizmī’’s ...
... Indian and Arabic Mathematics • India took Greek mathematics and developed early symbolic methods • Arab mathematicians extended and spread Indian algebra to Europe • The word "algebra" is named after the Arabic word "al-jabr" from the title of Persian mathematician Muhammad ibn Mūsā alkhwārizmī’’s ...
Solving Equations with Infinite or No Solutions Worksheet
... Name____________________________________ Date_____________ ...
... Name____________________________________ Date_____________ ...























