Geometry: Euclidean
... intersects the other two sides in two different points if and only if it divides these sides into segments that are proportional. (The “two different points” simply requires the point of intersection to not be the vertex.) Theorem 28: AAA Triangle Similarity. (E) If the interior angles of one triang ...
... intersects the other two sides in two different points if and only if it divides these sides into segments that are proportional. (The “two different points” simply requires the point of intersection to not be the vertex.) Theorem 28: AAA Triangle Similarity. (E) If the interior angles of one triang ...
Powerpoint
... There many situations in which the sum of the products “mass times velocity” is constant over time To each product we assign the name, “momentum” and associate it with a conservation law. (Units: kg m/s or N s) A force applied for a certain period of time can be graphed and the area under the cu ...
... There many situations in which the sum of the products “mass times velocity” is constant over time To each product we assign the name, “momentum” and associate it with a conservation law. (Units: kg m/s or N s) A force applied for a certain period of time can be graphed and the area under the cu ...
HSM12CC_GM_06_06_CM
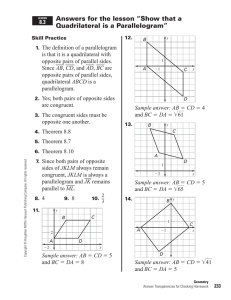
... Underline the correct word to complete each sentence. 1. An isosceles triangle always has two / three congruent sides. 2. An equilateral triangle is also a(n) isosceles / right triangle. 3. Cross out the length(s) that can NOT be side lengths of an isosceles triangle. ...
... Underline the correct word to complete each sentence. 1. An isosceles triangle always has two / three congruent sides. 2. An equilateral triangle is also a(n) isosceles / right triangle. 3. Cross out the length(s) that can NOT be side lengths of an isosceles triangle. ...
Electricity and Magnetism Review 1: Units 1-6
... Point charge +3Q at center of neutral conducting shell of inner radius r1 and outer radius r2. a) What is E everywhere? Use Gaussian surface = sphere centered on origin y Q r2 ...
... Point charge +3Q at center of neutral conducting shell of inner radius r1 and outer radius r2. a) What is E everywhere? Use Gaussian surface = sphere centered on origin y Q r2 ...
Document
... the work done by the conservative force is ∆U=-Wc.. The negative sign tells us that positive work by the conservative force leads to a decrease in potential energy. Therefore, the change in potential energy, associated with an infinitesimal displacement ds, is ...
... the work done by the conservative force is ∆U=-Wc.. The negative sign tells us that positive work by the conservative force leads to a decrease in potential energy. Therefore, the change in potential energy, associated with an infinitesimal displacement ds, is ...
Document
... At points A and B, construct AP ]› such that the angle each and BQ ray makes with the line is the same. Mark off congruent segments starting at points A and ]› and BQ ]›, respectively. B along AP Draw the line segment joining these two endpoints. ...
... At points A and B, construct AP ]› such that the angle each and BQ ray makes with the line is the same. Mark off congruent segments starting at points A and ]› and BQ ]›, respectively. B along AP Draw the line segment joining these two endpoints. ...
QFT on curved spacetimes: axiomatic framework and applications
... these degrees of freedom influence each other. This is the principle of locality, more precisely expressed by the German word Nahwirkungsprinzip. It states that each degree of freedom is influenced only by a relatively small number of other degrees of freedom. This induces a concept of neighborhood ...
... these degrees of freedom influence each other. This is the principle of locality, more precisely expressed by the German word Nahwirkungsprinzip. It states that each degree of freedom is influenced only by a relatively small number of other degrees of freedom. This induces a concept of neighborhood ...
Geometry - Asbury Park School District
... understand that the measure of an angle whose vertex lies in the interior of a circle is equal to half the sum of the angle measures of the arcs intercepted by it and its vertical angle find the measures of angles, arcs, and chords in figures that include two secant lines meeting outside a circle ( ...
... understand that the measure of an angle whose vertex lies in the interior of a circle is equal to half the sum of the angle measures of the arcs intercepted by it and its vertical angle find the measures of angles, arcs, and chords in figures that include two secant lines meeting outside a circle ( ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.