3D quantum mechanics, hydrogen atom
... In the 1D case, we had k = qπ/L, ψ(x) = (2/L)1/2 sin(qπx/L), and Eq = q2ħ2π2/2mL2, with q = 1, 2, 3... What happens now with the 3D case where ψ(x) = (2/L)3/2 sin(qπx/L) sin(rπy/L) sin(sπz/L)? The three directions are independent, so we will have kx = qπ/L, ψx(x) = (2/L)1/2sin(qπx/L), and Eqx = q2ħ2 ...
... In the 1D case, we had k = qπ/L, ψ(x) = (2/L)1/2 sin(qπx/L), and Eq = q2ħ2π2/2mL2, with q = 1, 2, 3... What happens now with the 3D case where ψ(x) = (2/L)3/2 sin(qπx/L) sin(rπy/L) sin(sπz/L)? The three directions are independent, so we will have kx = qπ/L, ψx(x) = (2/L)1/2sin(qπx/L), and Eqx = q2ħ2 ...
section 3.5-3.8 - Fulton County Schools
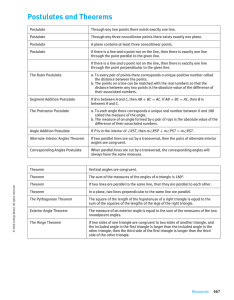
... • The Parallel Postulate – Given a line and a point not on the line, there is one and only one line that contains the give point and is parallel to the given line • Triangle Sum Theorem – The sum of the measures of the angles of a triangle is 180° ...
... • The Parallel Postulate – Given a line and a point not on the line, there is one and only one line that contains the give point and is parallel to the given line • Triangle Sum Theorem – The sum of the measures of the angles of a triangle is 180° ...
E3570: A particle on a disc with a homogeneous magnetic... levels
... (3) Write down the Hamiltonian in polar coordinates and identify the radial equation. (4) What are the energy levels determined by the radial equation without the Zeeman term? What is the degeneracy? (5) What are the energy levels determined by the radial equation with the Zeeman term? What is the d ...
... (3) Write down the Hamiltonian in polar coordinates and identify the radial equation. (4) What are the energy levels determined by the radial equation without the Zeeman term? What is the degeneracy? (5) What are the energy levels determined by the radial equation with the Zeeman term? What is the d ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.