Download 6-4 - Ithaca Public Schools

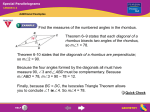
Name_____________________________________ Class____________________________ Date ________________
Lesson 6-4
Special Parallelograms
Lesson Objectives
1 Use properties of diagonals of
rhombuses and rectangles
2 Determine whether a parallelogram is
a rhombus or a rectangle
NAEP 2005 Strand: Geometry
Topic: Geometry
Local Standards: ____________________________________
All rights reserved.
Key Concepts.
Rhombuses
Theorem 6-9
B
AC bisects BAD, so bisects , so 3 4
1
2
A
Theorem 6-10
The diagonals of a rhombus are
4
D
C
.
A
Rectangles
Theorem 6-11
The diagonals of a rectangle are
C
B
'
© Pearson Education, Inc., publishing as Pearson Prentice Hall.
3
Each diagonal of a rhombus
D
A
D
B
C
.
Parallelograms
Theorem 6-12
If one diagonal of a parallelogram bisects two angles of the parallelogram, then
Theorem 6-13
If the diagonals of a parallelogram are perpendicular, then
Theorem 6-14
If the diagonals of a parallelogram are congruent, then
Daily Notetaking Guide
Geometry Lesson 6-4
117
Name_____________________________________ Class____________________________ Date________________
Examples.
1 Finding Angle Measures Find the measures of the
numbered angles in the rhombus.
Theorem 6-9 states that each diagonal of a rhombus
bisects two angles of the rhombus, so m1 78.
B
78
,
so m2 2
3
Theorem 6-10 states that
C
1
A
4
D
.
Because the four angles formed by the diagonals all must have measure 90,
3 and ABD must be
All rights reserved.
m3 90 78 . Because mABD 78,
.
Finally, because BC DC, the
allows you to conclude that 4. So m4 .
2 Finding Diagonal Length One diagonal of a rectangle has length 8x 2.
The other diagonal has length 5x 11. Find the length of each diagonal.
By Theorem 6-11, the diagonals of a rectangle are
Diagonals of a rectangle are congruent.
2
Subtract
from each side.
Subtract
x
Divide each side by
( )2
5x 11 5(
) 11 8x 2 8
The length of each diagonal is
from each side.
.
Substitute.
Substitute.
.
Quick Check.
1. Find the measures of the numbered angles in the rhombus.
50
1
4
118
Geometry Lesson 6-4
2
3
Daily Notetaking Guide
© Pearson Education, Inc., publishing as Pearson Prentice Hall.
11 .
Name_____________________________________ Class____________________________ Date ________________
Example.
3 Identifying Special Parallelograms The diagonals of ABCD are such that
AC 16 cm and BD 8 cm. Can you conclude that ABCD is a rhombus or
a rectangle? Explain.
ABCD
rectangle are
be a rectangle, because AC BD and the diagonals of a
(Theorem 6-11). ABCD may be a rhombus,
© Pearson Education, Inc., publishing as Pearson Prentice Hall.
All rights reserved.
but it may also not be one, depending on whether
(Theorem 6-10).
Quick Check.
2. Find the length of the diagonals of rectangle GFED if FD 5y 9
and GE = y 5.
F
E
G
D
3. A parallelogram has angles of 30°, 150°, 30°, and 150°. Can you conclude
that it is a rhombus or a rectangle? Explain.
Daily Notetaking Guide
Geometry Lesson 6-4
119