Matrices
... More generally we write aij for the entry in the ith row, jth column. Matrices come in different sizes. Since A has two rows and three columns, we call A a 2×3 or “2 by3” matrix. The size of a matrix determines what other matrices it can be added to or multiplied with. Matrices are equal if they are ...
... More generally we write aij for the entry in the ith row, jth column. Matrices come in different sizes. Since A has two rows and three columns, we call A a 2×3 or “2 by3” matrix. The size of a matrix determines what other matrices it can be added to or multiplied with. Matrices are equal if they are ...
The Inverse of a matrix
... vaguely, from high-school algebra. Recall also that the determinant of a matrix is a scalar. Let’s work a specific example: ...
... vaguely, from high-school algebra. Recall also that the determinant of a matrix is a scalar. Let’s work a specific example: ...
1 The Chain Rule - McGill Math Department
... are two transformations such that (x1 , x2 , · · · , xn ) = G(F (x1 , x2 , · · · , xn )) then the Jacobian matrices DF and DG are inverse to one another. This is because, if I(x1 , x2 , · · · , xn ) = (x1 , x2 , · · · , xn ) then DI is the identity matrix n × n matrix In . Hence, In = D(I) = D(F ◦ G ...
... are two transformations such that (x1 , x2 , · · · , xn ) = G(F (x1 , x2 , · · · , xn )) then the Jacobian matrices DF and DG are inverse to one another. This is because, if I(x1 , x2 , · · · , xn ) = (x1 , x2 , · · · , xn ) then DI is the identity matrix n × n matrix In . Hence, In = D(I) = D(F ◦ G ...
SIMG-616-20142 EXAM #1 2 October 2014
... (b) Evaluate the projection of any vector in the null subspace onto any vector “passed” by the system (c) Determine if the matrix is invertible and give reasons. 6. (40%) A shift-invariant operation acts on 4 samples of a function [] that may be represented as a 4-element vector x. For the “first ...
... (b) Evaluate the projection of any vector in the null subspace onto any vector “passed” by the system (c) Determine if the matrix is invertible and give reasons. 6. (40%) A shift-invariant operation acts on 4 samples of a function [] that may be represented as a 4-element vector x. For the “first ...
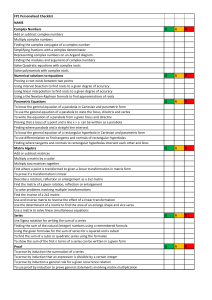
Updated Course Outline - Trinity College Dublin
... [ Sydsaeter, ch. 6 & 7 (up to 7.9) ] [ Chiang, ch. 6, 7.1 to 7.3, 8.1, 8.5 (up to p. 199), 9.3 & 9.5 ] 1. Definition and interpretation a. Difference quotient b. Derivative c. Increasing and decreasing functions d. Limits e. Continuity vs differentiability 2. Rules of Differentiation a. Constant fun ...
... [ Sydsaeter, ch. 6 & 7 (up to 7.9) ] [ Chiang, ch. 6, 7.1 to 7.3, 8.1, 8.5 (up to p. 199), 9.3 & 9.5 ] 1. Definition and interpretation a. Difference quotient b. Derivative c. Increasing and decreasing functions d. Limits e. Continuity vs differentiability 2. Rules of Differentiation a. Constant fun ...