Unit 5 Similarity and Triangles
... 1. How can you determine whether two figures are similar using similarity transformations, angle measures, and side lengths? 2. What is the AA Similarity theorem and why does it sufficiently determine whether two triangles are similar or not? 3. How can you prove that a line parallel to one side of ...
... 1. How can you determine whether two figures are similar using similarity transformations, angle measures, and side lengths? 2. What is the AA Similarity theorem and why does it sufficiently determine whether two triangles are similar or not? 3. How can you prove that a line parallel to one side of ...
Teacher Notes
... Supplementary angles – two angles whose measures have a sum of 180˚. Complementary angles – two angles whose measures have a sum of 90˚. Notes: Vertical angles are congruent. (This is the symbol for congruent, .) The sum of the measures of the angles in a linear pair is 180˚. means perpendicular ...
... Supplementary angles – two angles whose measures have a sum of 180˚. Complementary angles – two angles whose measures have a sum of 90˚. Notes: Vertical angles are congruent. (This is the symbol for congruent, .) The sum of the measures of the angles in a linear pair is 180˚. means perpendicular ...
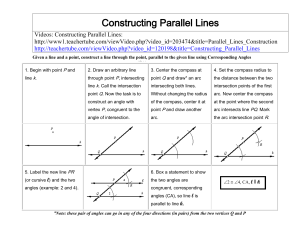
Constructing Parallel Lines
... Note: You should choose the points farther away to avoid crossing the measuring arcs. (3) Copy the angle inside B (1) to the opposite direction to point C (NE and SW along transversal BC) and to point A (NE and SW along transversal BA) (a) Make congruent measuring arcs in the same opposite directio ...
... Note: You should choose the points farther away to avoid crossing the measuring arcs. (3) Copy the angle inside B (1) to the opposite direction to point C (NE and SW along transversal BC) and to point A (NE and SW along transversal BA) (a) Make congruent measuring arcs in the same opposite directio ...