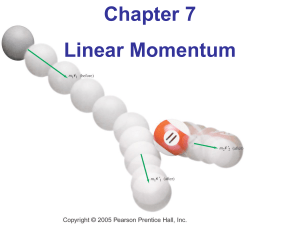
07-1 Note 07 Impulse and Momentum ∑ = ∑ =
... particle 2 is initially moving to the left then v2i must be given a negative sign. Eqs[7-13] are general expressions in that they describe two simpler special cases: 1 If m 1 = m2 then vif = v 2i and v2f = v 1i. In other words, if the particles have the same mass then they exchange speeds in the col ...
... particle 2 is initially moving to the left then v2i must be given a negative sign. Eqs[7-13] are general expressions in that they describe two simpler special cases: 1 If m 1 = m2 then vif = v 2i and v2f = v 1i. In other words, if the particles have the same mass then they exchange speeds in the col ...
9.1
... Vectors in the Coordinate Plane We now give analytic definitions of the various operations on vectors that we have described geometrically. Let’s start with equality of vectors. We’ve said that two vectors are equal if they have equal magnitude and the same direction. For the vectors u = a1, b1 a ...
... Vectors in the Coordinate Plane We now give analytic definitions of the various operations on vectors that we have described geometrically. Let’s start with equality of vectors. We’ve said that two vectors are equal if they have equal magnitude and the same direction. For the vectors u = a1, b1 a ...
Question Sheet 1 1. Let u = (−1,1,2) v = (2,0,3) w = (1,3,12
... (a) Find the area of the parallelogram F formed by u1 , u2 . (b) Convince yourself that the image of F under T , denoted T (F ), is the parallelogram formed by T (u1 ), T (u2 ). Then calculate the area of T (F ). (c) Find det(A). (d) Verify that Area(T (F ))/Area(F )=det(A). This is one conceptual d ...
... (a) Find the area of the parallelogram F formed by u1 , u2 . (b) Convince yourself that the image of F under T , denoted T (F ), is the parallelogram formed by T (u1 ), T (u2 ). Then calculate the area of T (F ). (c) Find det(A). (d) Verify that Area(T (F ))/Area(F )=det(A). This is one conceptual d ...
Linear Algebra for Theoretical Neuroscience (Part 2) 4 Complex
... • Show that e2πıJ = 1 for any real integer J. • Show that eıθ is periodic in θ with period 2π: that is, eıθ = eı(θ+2π) (Hint: recall that ea+b = ea eb for any a and b). Note that this implies that eıθ = eı(θ+2πJ) for any integer J. Again, multiplication by eıθ represents rotation through the angle θ ...
... • Show that e2πıJ = 1 for any real integer J. • Show that eıθ is periodic in θ with period 2π: that is, eıθ = eı(θ+2π) (Hint: recall that ea+b = ea eb for any a and b). Note that this implies that eıθ = eı(θ+2πJ) for any integer J. Again, multiplication by eıθ represents rotation through the angle θ ...
Notes - UMD Physics
... There is a special point in a system or object, called the center of mass (CM), that moves as if all of its mass (M = Σmi) is concentrated at that point ...
... There is a special point in a system or object, called the center of mass (CM), that moves as if all of its mass (M = Σmi) is concentrated at that point ...
Chapter 8:
... Use the above expression when the number of masses that make up a body is small. Use the moments of inertia in the table in the textbook for extended bodies. MFMcGraw-PHY 1401 ...
... Use the above expression when the number of masses that make up a body is small. Use the moments of inertia in the table in the textbook for extended bodies. MFMcGraw-PHY 1401 ...
Lecture 2
... This means for vectors formed by any two rows or any two columns Kronecker delta, which is 1 if i=j and 0 otherwise Image Registration ...
... This means for vectors formed by any two rows or any two columns Kronecker delta, which is 1 if i=j and 0 otherwise Image Registration ...
Solution
... (h) If A : V → V is a linear map, then the trace of A and A∗ coincide. Solution. (a) True. The ring of real numbers is a field, and any module over a field, that is any vector space, has a basis (on which it is free). (b) True. If a finite set S ⊆ M generates M, then the image of S in M/N is finite ...
... (h) If A : V → V is a linear map, then the trace of A and A∗ coincide. Solution. (a) True. The ring of real numbers is a field, and any module over a field, that is any vector space, has a basis (on which it is free). (b) True. If a finite set S ⊆ M generates M, then the image of S in M/N is finite ...