0: Ordinary Differential Equations - e
... x = −x in to Euler’s formula, noting that cos(−x) = cos(x) and sin(−x) = − sin(x) Linear combinations of complex exp. equivalent to linear combinations of sines and cosines. ...
... x = −x in to Euler’s formula, noting that cos(−x) = cos(x) and sin(−x) = − sin(x) Linear combinations of complex exp. equivalent to linear combinations of sines and cosines. ...
Summary of week 8 (Lectures 22, 23 and 24) This week we
... It is easy to generalize the above discussion to the complex case: it is simply necessary to take complex conjugates in a few places. Definition. If A is a matrix over the complex field then we define the conjugate of A to be the matrix A whose (i, j)-entry is the complex conjugate of the (i, j)-en ...
... It is easy to generalize the above discussion to the complex case: it is simply necessary to take complex conjugates in a few places. Definition. If A is a matrix over the complex field then we define the conjugate of A to be the matrix A whose (i, j)-entry is the complex conjugate of the (i, j)-en ...
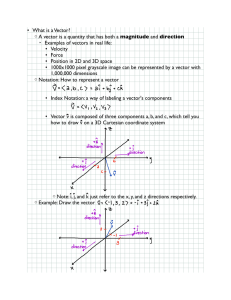
Linear Equations in Two Variables
... variables, we could take two different linear equations in two variables and ask for all those points that are solutions to both of the linear equations. For example, the point x = 4 and y = 1 is a solution to both of the equations x + y = 5 and x − y = 3. If you have more than one linear equation, ...
... variables, we could take two different linear equations in two variables and ask for all those points that are solutions to both of the linear equations. For example, the point x = 4 and y = 1 is a solution to both of the equations x + y = 5 and x − y = 3. If you have more than one linear equation, ...
1 Lines 2 Linear systems of equations
... STEP 1 Select two equations from the system and eliminate a variable from them. STEP 2 If there are additional equations in the system, pair off equations and eliminate the same variable from them. STEP 3 Continue Steps 1 and 2 on successive systems until one equation containing one variable remains. ...
... STEP 1 Select two equations from the system and eliminate a variable from them. STEP 2 If there are additional equations in the system, pair off equations and eliminate the same variable from them. STEP 3 Continue Steps 1 and 2 on successive systems until one equation containing one variable remains. ...
3.1 Extra Practice (Homework)
... Graph Linear Equations The graph of a linear equations represents all the solutions of the equation. An x-coordinate of the point at which a graph of an equation crosses the x-axis in an x-intercept. A y-coordinate of the point at which a graph crosses the y-axis is called a y-intercept. ...
... Graph Linear Equations The graph of a linear equations represents all the solutions of the equation. An x-coordinate of the point at which a graph of an equation crosses the x-axis in an x-intercept. A y-coordinate of the point at which a graph crosses the y-axis is called a y-intercept. ...
Student Learning Outcomes
... a. To graph a function and find/determine (x-and y-intercepts, zeros, intervals on which the function is increasing and decreasing, maximum and minimum and local minima and maxima, obtain information from or about the graph of a function b. Regression Program to find the Curve of Best Fit (linear, q ...
... a. To graph a function and find/determine (x-and y-intercepts, zeros, intervals on which the function is increasing and decreasing, maximum and minimum and local minima and maxima, obtain information from or about the graph of a function b. Regression Program to find the Curve of Best Fit (linear, q ...
hp calculators
... The HP 35s two build-in solver equations to find solutions to 2x2 and 3x3 linear systems. These can detect situations where no solution exists or where an infinite number of solutions exist. These solver equations are part of the HP 35s ROM and are always present at the top of the equation list. If ...
... The HP 35s two build-in solver equations to find solutions to 2x2 and 3x3 linear systems. These can detect situations where no solution exists or where an infinite number of solutions exist. These solver equations are part of the HP 35s ROM and are always present at the top of the equation list. If ...
Linear algebra
Linear algebra is the branch of mathematics concerning vector spaces and linear mappings between such spaces. It includes the study of lines, planes, and subspaces, but is also concerned with properties common to all vector spaces.The set of points with coordinates that satisfy a linear equation forms a hyperplane in an n-dimensional space. The conditions under which a set of n hyperplanes intersect in a single point is an important focus of study in linear algebra. Such an investigation is initially motivated by a system of linear equations containing several unknowns. Such equations are naturally represented using the formalism of matrices and vectors.Linear algebra is central to both pure and applied mathematics. For instance, abstract algebra arises by relaxing the axioms of a vector space, leading to a number of generalizations. Functional analysis studies the infinite-dimensional version of the theory of vector spaces. Combined with calculus, linear algebra facilitates the solution of linear systems of differential equations.Techniques from linear algebra are also used in analytic geometry, engineering, physics, natural sciences, computer science, computer animation, and the social sciences (particularly in economics). Because linear algebra is such a well-developed theory, nonlinear mathematical models are sometimes approximated by linear models.