Honors Precalculus Modeling Using Exponential and Logarithmic
... Many real-world phenomena can be modeled using exponential functions, specifically those types of populations which grow as a proportion of itself over time. In fact, that is the hallmark of an exponential growth or decay function. Examples include. Compound interest – Calculating the amount of mone ...
... Many real-world phenomena can be modeled using exponential functions, specifically those types of populations which grow as a proportion of itself over time. In fact, that is the hallmark of an exponential growth or decay function. Examples include. Compound interest – Calculating the amount of mone ...
Intravenous Infusion Equations
... If the infusion did not run until steady state was achieved, it is still possible to compute pharmacokinetic parameters from postinfusion concentrations. In the following example, a patient was given a single 120-mg dose of tobramycin as a 60-minute infusion, and concentrations at the end of infusio ...
... If the infusion did not run until steady state was achieved, it is still possible to compute pharmacokinetic parameters from postinfusion concentrations. In the following example, a patient was given a single 120-mg dose of tobramycin as a 60-minute infusion, and concentrations at the end of infusio ...
Worms
... • Period before which it is unsafe (illegal) to slaughter for meat or use milk or eggs for human consumption because of chemical residues. • For some compounds, there is NO withholding period, meaning the levels in the product never reach threshold levels. • The withholding period is calculated by c ...
... • Period before which it is unsafe (illegal) to slaughter for meat or use milk or eggs for human consumption because of chemical residues. • For some compounds, there is NO withholding period, meaning the levels in the product never reach threshold levels. • The withholding period is calculated by c ...
Supplementary Text 1
... form, which has greater advantages for algebraic analyses about the steady state that are only of secondary importance here. ...
... form, which has greater advantages for algebraic analyses about the steady state that are only of secondary importance here. ...
Falling body problems
... • If y is the distance traveled, then the velocity is v = dy/dt and acceleration is a = d2y/dt2 • Newton’s second law can be adapted to ...
... • If y is the distance traveled, then the velocity is v = dy/dt and acceleration is a = d2y/dt2 • Newton’s second law can be adapted to ...
1) In the reaction H2O + CH3COOH H3O+ +
... Numerical Problems. You must show all your work for complete credit. 6) (20 points) Consider an aqueous solution which contains 0.010 M acetic acid (CH3COOH), 0.010 M sodium acetate (Na+ CH3COO-) and 0.010 M sodium chloride (Na+ Cl-). The pKA of acetic acid is 4.75. a) Assuming that all activity co ...
... Numerical Problems. You must show all your work for complete credit. 6) (20 points) Consider an aqueous solution which contains 0.010 M acetic acid (CH3COOH), 0.010 M sodium acetate (Na+ CH3COO-) and 0.010 M sodium chloride (Na+ Cl-). The pKA of acetic acid is 4.75. a) Assuming that all activity co ...
Fitness Room Study Guide Aerobic activity: uses oxygen to supply
... -how often you exercise. Ex. Children and adolescents should get 60 minutes of physical activity a day 5-6 days a week. I-Intensity -how hard a person exercises. Ex. % heart rate or intensity of exercise increase slowly, over time for improved fitness T- Time - total amount of time spent on one exer ...
... -how often you exercise. Ex. Children and adolescents should get 60 minutes of physical activity a day 5-6 days a week. I-Intensity -how hard a person exercises. Ex. % heart rate or intensity of exercise increase slowly, over time for improved fitness T- Time - total amount of time spent on one exer ...
equations for ap biology - Bremen High School District 228
... When you calculate growth rates with this equation and start with N near 0, you can plot a curve called a sigmoid curve (x-axis is time, y-axis is population size), which grows quickly at first, but the rate of increase drops off until it hits zero, at which there is no more increase in N. Due to th ...
... When you calculate growth rates with this equation and start with N near 0, you can plot a curve called a sigmoid curve (x-axis is time, y-axis is population size), which grows quickly at first, but the rate of increase drops off until it hits zero, at which there is no more increase in N. Due to th ...
Physics on Friday - elyceum
... • Joe runs with a constant velocity of 5.4 m/s for 20 s before he reaches a pile of leaves. It takes 1.5 s for Joe to come to a stop in the pile. What is his rate of acceleration in the leaf pile and how far did Joe travel overall? ...
... • Joe runs with a constant velocity of 5.4 m/s for 20 s before he reaches a pile of leaves. It takes 1.5 s for Joe to come to a stop in the pile. What is his rate of acceleration in the leaf pile and how far did Joe travel overall? ...
Half-Life
... Half-Life: The time it takes a substance to decrease to half of a previous value. Half-Life is a good predictor of how long a substance will exist. Drug Half-Life: The time required for the total amount of a drug in blood to diminish by half, once the drug reaches its peak concentration. See P ...
... Half-Life: The time it takes a substance to decrease to half of a previous value. Half-Life is a good predictor of how long a substance will exist. Drug Half-Life: The time required for the total amount of a drug in blood to diminish by half, once the drug reaches its peak concentration. See P ...
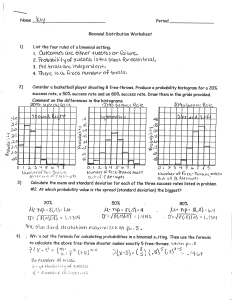
Binomial Dist Answers
... 4). . Wr, :e out the formula for calculating probabilities in a binomial sÿfting. Then use the formula to calculate the above free-throw shooter makes exactly 5 free-throws, voh €_ÿ e-_, ...
... 4). . Wr, :e out the formula for calculating probabilities in a binomial sÿfting. Then use the formula to calculate the above free-throw shooter makes exactly 5 free-throws, voh €_ÿ e-_, ...
Drug removal rate
... So if the drug is only filtered out at the glomerulus, and all of the filtered drug is excreted into the urine (not secreted or reabsorbed in the tubules), then the rate of drug excretion (refers to urine) is the same as the drug removal rate at the glomerulus, or: CLrenal = fu x GFR, and if the dr ...
... So if the drug is only filtered out at the glomerulus, and all of the filtered drug is excreted into the urine (not secreted or reabsorbed in the tubules), then the rate of drug excretion (refers to urine) is the same as the drug removal rate at the glomerulus, or: CLrenal = fu x GFR, and if the dr ...
Slide 1 - Beachwood City Schools
... We were asked if the traffic flow was increasing or decreasing at t=7. For this, we’ll need the derivative. F’(t) = 2 cos (t/2) ...
... We were asked if the traffic flow was increasing or decreasing at t=7. For this, we’ll need the derivative. F’(t) = 2 cos (t/2) ...