atomsagain
... To describe one electron, we give the following information: •n – this is called the shell Shells are labeled by numbers 1, 2, 3, . . . •l – this is called the subshell Subshells are denoted by letter s, p, d, f, g •m – this is called the orbital orbital depends on choice of axes •ms – this is ...
... To describe one electron, we give the following information: •n – this is called the shell Shells are labeled by numbers 1, 2, 3, . . . •l – this is called the subshell Subshells are denoted by letter s, p, d, f, g •m – this is called the orbital orbital depends on choice of axes •ms – this is ...
... Since the discrete energy levels are very close to each other, we do not consider the occupation of the individual levels but the occupation of the total number of energy values between ei and ei + dei. The number of energy levels between ei and e i + de i: Ai. These are occupied by Ni species. For ...
The Impact of Special Relativity in Nuclear Physics: It`s not just E=Mc 2
... Guiding Principles of Special Relativity 1) The speed of light c, is a constant for all observers in inertial reference frames. 2) The laws of physics must remain invariant in form in all inertial reference frames. ...
... Guiding Principles of Special Relativity 1) The speed of light c, is a constant for all observers in inertial reference frames. 2) The laws of physics must remain invariant in form in all inertial reference frames. ...
Density Matrix
... term “state” refers to a thermodynamic state, i. e. macroscopic variables such as pressure, temperature, density etc needed to specify a system, are given. In mechanics, of course, state variables are microscopic, and a state is specified by giving the positions and velocities of all particles as a ...
... term “state” refers to a thermodynamic state, i. e. macroscopic variables such as pressure, temperature, density etc needed to specify a system, are given. In mechanics, of course, state variables are microscopic, and a state is specified by giving the positions and velocities of all particles as a ...
Wave Packets - Centro de Física Teórica
... the position x = ω̄ ′t at the instant of time t. Consequently, for ω linear in k as in formula (21), the wave packet moves with a constant velocity ω̄ ′ and hence represents a freely moving particle. The general idea is depicted in figure (2). Notice, that for ω linear in k as in formula (21), the w ...
... the position x = ω̄ ′t at the instant of time t. Consequently, for ω linear in k as in formula (21), the wave packet moves with a constant velocity ω̄ ′ and hence represents a freely moving particle. The general idea is depicted in figure (2). Notice, that for ω linear in k as in formula (21), the w ...
学术报告
... energy, the fidelity susceptibility shows distinct scaling and singular behaviours around the critical point. Secondly, I would like to introduce the relation between the fidelity susceptibility and quantum adiabatic theorem. For a d-dimensional quantum many-body system, we show that the duration ti ...
... energy, the fidelity susceptibility shows distinct scaling and singular behaviours around the critical point. Secondly, I would like to introduce the relation between the fidelity susceptibility and quantum adiabatic theorem. For a d-dimensional quantum many-body system, we show that the duration ti ...
Example 27-1
... •When electron changes to a lower n it emits a photon of energy equal to the energy difference. •Electron must be given energy to move to a higher n •This formula can be used for any single electron atom or ion such as a singly-ionized He ion in which case Z=2. •The radius of the orbit is given by C ...
... •When electron changes to a lower n it emits a photon of energy equal to the energy difference. •Electron must be given energy to move to a higher n •This formula can be used for any single electron atom or ion such as a singly-ionized He ion in which case Z=2. •The radius of the orbit is given by C ...
PPT - University of Washington
... and |01> are not eigenstates. These states are rotated. After a time pi*hbar/2*J, we have performed half of a swap operation. This is a known universal quantum gate ...
... and |01> are not eigenstates. These states are rotated. After a time pi*hbar/2*J, we have performed half of a swap operation. This is a known universal quantum gate ...
Exam #: Printed Name: Signature: PHYSICS DEPARTMENT
... momentum (L), total spin (S ), and total angular momentum (J )|for example, as in n 2S+1LJ = 2 3 S1. What are the labels n 2S+1 LJ for each of the six states? c. Consider the transitions from each of the six states of b. to the ground state, 1 1S0, by electric dipole radiation. Which transitions are ...
... momentum (L), total spin (S ), and total angular momentum (J )|for example, as in n 2S+1LJ = 2 3 S1. What are the labels n 2S+1 LJ for each of the six states? c. Consider the transitions from each of the six states of b. to the ground state, 1 1S0, by electric dipole radiation. Which transitions are ...
Document
... • Weak measurements shed light on Hardy's Paradox as well • "Weak probabilities" obey all the constraints we expected in that example. • There is no contradiction, because if negative "probabilities" are accepted, all the joint probabilities can be constructed. ...
... • Weak measurements shed light on Hardy's Paradox as well • "Weak probabilities" obey all the constraints we expected in that example. • There is no contradiction, because if negative "probabilities" are accepted, all the joint probabilities can be constructed. ...
Document
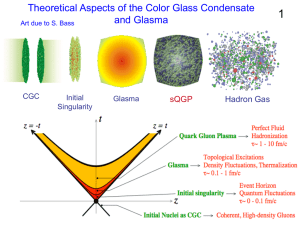
... What is the Color Glass Condensate? Glue at large x generates glue at small x Glue at small x is classical field Time dilation -> Classical field is glassy High phase space density -> Condensate Phase space density: Attractive potential ...
... What is the Color Glass Condensate? Glue at large x generates glue at small x Glue at small x is classical field Time dilation -> Classical field is glassy High phase space density -> Condensate Phase space density: Attractive potential ...
Quantum Mechanics
... The question of the distances between the planets used to be the biggest open problem in science. But we now know that it’s a complicated question that isn’t answered by the fundamental theory. ...
... The question of the distances between the planets used to be the biggest open problem in science. But we now know that it’s a complicated question that isn’t answered by the fundamental theory. ...
Particle in a box

In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example a ball trapped inside a large box, the particle can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow (on the scale of a few nanometers), quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never ""sit still"". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.The particle in a box model provides one of the very few problems in quantum mechanics which can be solved analytically, without approximations. This means that the observable properties of the particle (such as its energy and position) are related to the mass of the particle and the width of the well by simple mathematical expressions. Due to its simplicity, the model allows insight into quantum effects without the need for complicated mathematics. It is one of the first quantum mechanics problems taught in undergraduate physics courses, and it is commonly used as an approximation for more complicated quantum systems.