
Gravity Newton`s Law of Universal Gravitation states that every
... (on a point particle) and we will look at this attraction when we are both outside and inside the sphere.. We will first look at the case when the particle m is at a distance r outside a solid sphere of radius R and mass M. We will consider the large mass to be constructed of a collections of thin s ...
... (on a point particle) and we will look at this attraction when we are both outside and inside the sphere.. We will first look at the case when the particle m is at a distance r outside a solid sphere of radius R and mass M. We will consider the large mass to be constructed of a collections of thin s ...
WorkPowerEnergy
... • Identify several forms of energy • Calculate kinetic energy for an object • Apply in the work-kinetic energy theorem to solve problems • Distinguish between kinetic and potential energy • Classify different types of potential energy • Calculate the potential energy associated with an object’s posi ...
... • Identify several forms of energy • Calculate kinetic energy for an object • Apply in the work-kinetic energy theorem to solve problems • Distinguish between kinetic and potential energy • Classify different types of potential energy • Calculate the potential energy associated with an object’s posi ...
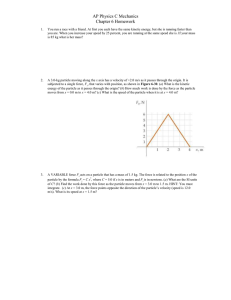
Chapter 6 Homework
... You run a race with a friend. At first you each have the same kinetic energy, but she is running faster than you are. When you increase your speed by 25 percent, you are running at the same speed she is. If your mass is 85 kg what is her mass? ...
... You run a race with a friend. At first you each have the same kinetic energy, but she is running faster than you are. When you increase your speed by 25 percent, you are running at the same speed she is. If your mass is 85 kg what is her mass? ...
Energy, Work and Simple Machines
... • W=Fd (work is measured in joules too. One joule of work is done when a force of 1N acts on an object over a displacement of 1m. ) – Holds only for constant forces exerted in the direction of motion – What happens if the force exerted is perpendicular to the direction of the object? – Consider a pl ...
... • W=Fd (work is measured in joules too. One joule of work is done when a force of 1N acts on an object over a displacement of 1m. ) – Holds only for constant forces exerted in the direction of motion – What happens if the force exerted is perpendicular to the direction of the object? – Consider a pl ...
SAMPLE QUESTION PAPER 2015 – I, 2015 SCIENCE Class – IX
... (ii) mass of one object is increased four times (iii) distance is reduced to one fourth. 23. State Newton’s first law of motion. Show that Newton’s first law of motion is a special case of Newton’s second law. Determine the acceleration of a car of mass 800 kg, on application of a force of 200 N on ...
... (ii) mass of one object is increased four times (iii) distance is reduced to one fourth. 23. State Newton’s first law of motion. Show that Newton’s first law of motion is a special case of Newton’s second law. Determine the acceleration of a car of mass 800 kg, on application of a force of 200 N on ...
Motion and Potential Energy Graphs
... object downwards with acceleration g. As it does so it will lose potential energy P Eg and gain kinetic energy KE in such a way that its total mechanical energy ME remains constant. This motion can be deduced by looking at the potential-energy graph using the two concepts outlined above. Initially K ...
... object downwards with acceleration g. As it does so it will lose potential energy P Eg and gain kinetic energy KE in such a way that its total mechanical energy ME remains constant. This motion can be deduced by looking at the potential-energy graph using the two concepts outlined above. Initially K ...
Rotational Motion
... A plumber slips a piece of scrap pipe over his wrench handle to help loosing a pipe fitting. He then applies his full weight (900 N) to the end of the pipe by standing on it. The distance from the fitting to his foot is 0.8 m, and the wrench and pipe make a 19º angle with the ground. Find the magnit ...
... A plumber slips a piece of scrap pipe over his wrench handle to help loosing a pipe fitting. He then applies his full weight (900 N) to the end of the pipe by standing on it. The distance from the fitting to his foot is 0.8 m, and the wrench and pipe make a 19º angle with the ground. Find the magnit ...
Review Game - SCHOOLinSITES
... Which of the following statements is correct? a. The farther the force is from the axis of rotation, the more torque is produced. b. The closer the force is to the axis of rotation, the more torque is produced. c. The closer the force is to the axis of rotation, the easier it is to rotate the object ...
... Which of the following statements is correct? a. The farther the force is from the axis of rotation, the more torque is produced. b. The closer the force is to the axis of rotation, the more torque is produced. c. The closer the force is to the axis of rotation, the easier it is to rotate the object ...
The Momentum Principle
... The Momentum Principle An object moves in a straight line and at constant speed except to the extent that it interacts with other objects ...
... The Momentum Principle An object moves in a straight line and at constant speed except to the extent that it interacts with other objects ...




![06 Momentum WS 08 [v6.0]](http://s1.studyres.com/store/data/017198328_1-636fbdb6d6c62db5233df770cc2cf61d-300x300.png)

















