Notes on Binomial Theorem
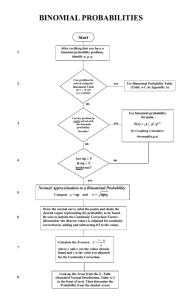
... There are charts as well – but only for some probabilities so you need to know the formula. ...
... There are charts as well – but only for some probabilities so you need to know the formula. ...
Document
... (a) What is the probability that two particular people A and B will be seated next to each other? (b) What is the probability that k particular people will occupy k adjacent seats in the row? A box contains 24 light bulbs of which four are defective. If one person select 10 bulbs from the box in a r ...
... (a) What is the probability that two particular people A and B will be seated next to each other? (b) What is the probability that k particular people will occupy k adjacent seats in the row? A box contains 24 light bulbs of which four are defective. If one person select 10 bulbs from the box in a r ...
QUIZ 4-Independent and Conditional
... 2) Decide if the events are mutually exclusive or overlapping and then find P(AUB) a) A = Rolling a 2 on a regular six-sided die B = Rolling an odd number on a regular six-sided die ...
... 2) Decide if the events are mutually exclusive or overlapping and then find P(AUB) a) A = Rolling a 2 on a regular six-sided die B = Rolling an odd number on a regular six-sided die ...
Probability
... dependent events conditional probability permutations combinations Venn diagrams ...
... dependent events conditional probability permutations combinations Venn diagrams ...
1. Each occasion upon which we observe a random phenomenon is
... 3. When the probability comes from the long run relative frequency of the event’s occurrence, it is called a(n) A. theoretical probability. ...
... 3. When the probability comes from the long run relative frequency of the event’s occurrence, it is called a(n) A. theoretical probability. ...
Chapter 4 - morgansmathmarvels
... Ex. 1 Human eye color is controlled by a single pair of genes (one from each parent). Brown eyed color, B, is dominant over blue eyed color, b. Therefore if a person has Bb, then the brown dominates and they have brown eyes. Mother Father ...
... Ex. 1 Human eye color is controlled by a single pair of genes (one from each parent). Brown eyed color, B, is dominant over blue eyed color, b. Therefore if a person has Bb, then the brown dominates and they have brown eyes. Mother Father ...
7501 (Probability and Statistics)
... The aim of the course is to introduce students to the theory of probability and some of the statistical methods based upon it. Many physical processes involve random components which can only be modelled using probabilistic methods. Statistical theory is vital for analysing scientific data where it ...
... The aim of the course is to introduce students to the theory of probability and some of the statistical methods based upon it. Many physical processes involve random components which can only be modelled using probabilistic methods. Statistical theory is vital for analysing scientific data where it ...
Conditional probability and independence Bernoulli trials and the
... Independence of more than two events: Surprisingly, there are situations in which three or more events are independent of each other in pairs but are not independent of one another more generally. See the bottom of page 24 for an example. Events A1 , A2 , A3 , ... are independent if and only if the ...
... Independence of more than two events: Surprisingly, there are situations in which three or more events are independent of each other in pairs but are not independent of one another more generally. See the bottom of page 24 for an example. Events A1 , A2 , A3 , ... are independent if and only if the ...
Ars Conjectandi

Ars Conjectandi (Latin for The Art of Conjecturing) is a book on combinatorics and mathematical probability written by Jakob Bernoulli and published in 1713, eight years after his death, by his nephew, Niklaus Bernoulli. The seminal work consolidated, apart from many combinatorial topics, many central ideas in probability theory, such as the very first version of the law of large numbers: indeed, it is widely regarded as the founding work of that subject. It also addressed problems that today are classified in the twelvefold way, and added to the subjects; consequently, it has been dubbed an important historical landmark in not only probability but all combinatorics by a plethora of mathematical historians. The importance of this early work had a large impact on both contemporary and later mathematicians; for example, Abraham de Moivre.Bernoulli wrote the text between 1684 and 1689, including the work of mathematicians such as Christiaan Huygens, Gerolamo Cardano, Pierre de Fermat, and Blaise Pascal. He incorporated fundamental combinatorial topics such as his theory of permutations and combinations—the aforementioned problems from the twelvefold way—as well as those more distantly connected to the burgeoning subject: the derivation and properties of the eponymous Bernoulli numbers, for instance. Core topics from probability, such as expected value, were also a significant portion of this important work.