Predictions For Cooling A Solid To Its Ground State
... therefore predictions (P1 )-(P2 ) of the Bose-Einstein equation are false. To prove this claim we analyze the Einstein model of a solid [2]. The Einstein model is based on the following assumptions: (A1) Each of the N atoms in the lattice of the solid is a 3D quantum harmonic oscillator, and q > 0 q ...
... therefore predictions (P1 )-(P2 ) of the Bose-Einstein equation are false. To prove this claim we analyze the Einstein model of a solid [2]. The Einstein model is based on the following assumptions: (A1) Each of the N atoms in the lattice of the solid is a 3D quantum harmonic oscillator, and q > 0 q ...
Lecture 2 - Department of Applied Physics
... May be that are not paradoxes and is a real situation. One of the indirect supports of this assertion is the example with «spin echo». It is known that the changing of the direction of magnet particle motion under the influence of magnetic fields leads in some time to the non-Equilibrium State wher ...
... May be that are not paradoxes and is a real situation. One of the indirect supports of this assertion is the example with «spin echo». It is known that the changing of the direction of magnet particle motion under the influence of magnetic fields leads in some time to the non-Equilibrium State wher ...
Spin Current - Columbia Physics
... Spintronics is not just a new type of electronics in the 21th century [1,2] but provides a variety of new physics [3]. The flow of electron spin, the so-called “spin current”, is a key concept in spintronics. When the spin current interacts with the magnetic moment in a ferromagnetic metal, the angu ...
... Spintronics is not just a new type of electronics in the 21th century [1,2] but provides a variety of new physics [3]. The flow of electron spin, the so-called “spin current”, is a key concept in spintronics. When the spin current interacts with the magnetic moment in a ferromagnetic metal, the angu ...
4.3 Ferromagnetism The Mean Field Approach 4.3.1 Mean Field Theory of Ferromagnetism
... a spontaneous large magnetic polarization without an external magnetic field as the first big result of the mean field theory. We can do much more with the mean field theory, however. First, we note that switching on an external magnetic field does not have a large effect. J increases somewhat, but ...
... a spontaneous large magnetic polarization without an external magnetic field as the first big result of the mean field theory. We can do much more with the mean field theory, however. First, we note that switching on an external magnetic field does not have a large effect. J increases somewhat, but ...
4– Quantum Mechanical Description of NMR 4.1 Mathematical Tools∗
... In this case, we have many ψn (x) with n = 1, 2, . . .. This is analogous to the particle in a one-dimensional box problem, where the wavefunction ψn (x) describes the microstate of a quantum particle of mass m in a box of length L (x ∈ [0 . . . L]) for every discrete energy level En , n = 1, 2, . . ...
... In this case, we have many ψn (x) with n = 1, 2, . . .. This is analogous to the particle in a one-dimensional box problem, where the wavefunction ψn (x) describes the microstate of a quantum particle of mass m in a box of length L (x ∈ [0 . . . L]) for every discrete energy level En , n = 1, 2, . . ...
Lecture 20
... Note that the summation condition over and u does not allow this interaction to flip the spins. This is expected at first order for slow moving electrons, since they will only interact via the electric field, which we know from the atom does not continually flip spins. However, at higher energy spin ...
... Note that the summation condition over and u does not allow this interaction to flip the spins. This is expected at first order for slow moving electrons, since they will only interact via the electric field, which we know from the atom does not continually flip spins. However, at higher energy spin ...
Ambiguous model learning made unambiguous with 1/f priors
... opposite limit (strong-coupling) using the instanton method[5,6]. Arguably what we have really shown is that even if one starts with weak coupling, so that it should be ”easy” to jump from one interpretation to another, for b > b∗ we will flow to strong-coupling, at which point known results about l ...
... opposite limit (strong-coupling) using the instanton method[5,6]. Arguably what we have really shown is that even if one starts with weak coupling, so that it should be ”easy” to jump from one interpretation to another, for b > b∗ we will flow to strong-coupling, at which point known results about l ...
PDF Version - Physics (APS)
... Vojta, Kotabage, and Hoyos have shown that a similar real-space analysis applies quite generally to dissipative disordered chains on the verge of a symmetrybreaking phase transition. Their focus is on a system that is similar to a chain of dynamically fluctuating magnetons (magnetic moments that can ...
... Vojta, Kotabage, and Hoyos have shown that a similar real-space analysis applies quite generally to dissipative disordered chains on the verge of a symmetrybreaking phase transition. Their focus is on a system that is similar to a chain of dynamically fluctuating magnetons (magnetic moments that can ...
+1 0 - The Dionne Group
... 2. L_Rule: For a term of a ggiven multiplicity, the greatest value of L lies lowest in energy if L is high, the electrons can effectively avoid each other 3. J-Rule: if subshell is less than half filled, lowest J is lowest energy. If greater than half filled, highest J is lowest energy q to half-f ...
... 2. L_Rule: For a term of a ggiven multiplicity, the greatest value of L lies lowest in energy if L is high, the electrons can effectively avoid each other 3. J-Rule: if subshell is less than half filled, lowest J is lowest energy. If greater than half filled, highest J is lowest energy q to half-f ...
Electrons in graphene - Condensed Matter Physics
... Since the wavefunctions have phases ±φ/2, they change phase by π when θ increases by 2π, that is, when the -vector goes once around a loop surrounding a K point. The code words “massless Dirac spectrum” are used to refer to the linear ε versus k relation, and the special points Ki are called the “Di ...
... Since the wavefunctions have phases ±φ/2, they change phase by π when θ increases by 2π, that is, when the -vector goes once around a loop surrounding a K point. The code words “massless Dirac spectrum” are used to refer to the linear ε versus k relation, and the special points Ki are called the “Di ...
Recent progress in the theory of Anderson localization
... Change the shape of samples and see how wave functions change. ...
... Change the shape of samples and see how wave functions change. ...
General properties of overlap operators in disordered quantum spin
... In this paper, we study short-range quantum spin models with random interactions in d-dimensional cubic lattice ΛL = Zd ∩ [1, L]d . To define short-range interactions, we construct a collection CL of interaction ranges in the following way. Let m be an arbitrarily fixed positive integer independent ...
... In this paper, we study short-range quantum spin models with random interactions in d-dimensional cubic lattice ΛL = Zd ∩ [1, L]d . To define short-range interactions, we construct a collection CL of interaction ranges in the following way. Let m be an arbitrarily fixed positive integer independent ...
Spin-current and other unusual phases in magnetized triangular lattice antiferromagnets
... forbidden at low orders in perturbation theory [2]. As a consequence, the triplet band is very flat, a striking fact observed by neutron scattering experiments [13]. Since the triplets are very massive particles, it is natural to expect that they can crystallize at finite density, and it has been pr ...
... forbidden at low orders in perturbation theory [2]. As a consequence, the triplet band is very flat, a striking fact observed by neutron scattering experiments [13]. Since the triplets are very massive particles, it is natural to expect that they can crystallize at finite density, and it has been pr ...
Temperature and sample dependence of spin echo in SiC
... • Sample placed directly on the copper cold finger ...
... • Sample placed directly on the copper cold finger ...
Transition Metals and Coordination Chemistry - pp. 92-114
... Orbitals point between ligands weaker repulsion lower energy ...
... Orbitals point between ligands weaker repulsion lower energy ...
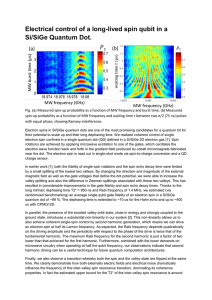
Electrical control of a long-lived spin qubit in a
... by a small splitting of the lowest two valleys. By changing the direction and magnitude of the external magnetic field as well as the gate voltages that define the dot potential, we were able to increase the valley splitting and also the difference in Zeeman splittings associated with these two vall ...
... by a small splitting of the lowest two valleys. By changing the direction and magnitude of the external magnetic field as well as the gate voltages that define the dot potential, we were able to increase the valley splitting and also the difference in Zeeman splittings associated with these two vall ...
Advanced Physical Chemistry
... UHF formalism. The HF procedure works well for atoms due to spherical symmetry, but for molecules, this symmetry is not there. Must expand the spatial parts of the spinorbitals in terms of another basis set. From a set of M basis functions , obtain M linearly independent spatial wavefunctions. End u ...
... UHF formalism. The HF procedure works well for atoms due to spherical symmetry, but for molecules, this symmetry is not there. Must expand the spatial parts of the spinorbitals in terms of another basis set. From a set of M basis functions , obtain M linearly independent spatial wavefunctions. End u ...
Atomic Term Symbols
... conceptually simple. If one uses relatively small CI matrices with the purpose to resolve the degeneracies that would occur without electron interaction the method is often called CASSCF, since we also want to optimize the orbitals in the electron configuration (Complete Active Space Self-Consistent ...
... conceptually simple. If one uses relatively small CI matrices with the purpose to resolve the degeneracies that would occur without electron interaction the method is often called CASSCF, since we also want to optimize the orbitals in the electron configuration (Complete Active Space Self-Consistent ...
ppt
... Resonant coupling in both metastable and ground state is Possible in a magnetic fieldsuch that the Zeemann effect in the metastable compensates the light shift of level 1 ...
... Resonant coupling in both metastable and ground state is Possible in a magnetic fieldsuch that the Zeemann effect in the metastable compensates the light shift of level 1 ...
E3570: A particle on a disc with a homogeneous magnetic... levels
... (3) Write down the Hamiltonian in polar coordinates and identify the radial equation. (4) What are the energy levels determined by the radial equation without the Zeeman term? What is the degeneracy? (5) What are the energy levels determined by the radial equation with the Zeeman term? What is the d ...
... (3) Write down the Hamiltonian in polar coordinates and identify the radial equation. (4) What are the energy levels determined by the radial equation without the Zeeman term? What is the degeneracy? (5) What are the energy levels determined by the radial equation with the Zeeman term? What is the d ...
A straightforward way to determine relative intensities of spin
... 1nuclear spins for each of t h e n equivalent atoms and evaluating relative intensities by counting the number of comhinations that vield the same net suin. One wav- of eeneratine all such possible spin states is t o k i t e the set of nuclear spins as a ~olvnomialand then raise the ~olvnomialto a D ...
... 1nuclear spins for each of t h e n equivalent atoms and evaluating relative intensities by counting the number of comhinations that vield the same net suin. One wav- of eeneratine all such possible spin states is t o k i t e the set of nuclear spins as a ~olvnomialand then raise the ~olvnomialto a D ...