Physics 137B
... Suppose you’re given a quantum system whose Hamiltonian H0 admits two eigenstates, ψa (with energy Ea ), and ψb (with energy Eb ). They are orthogonal, normalized, and non-degenerate (assume Ea is the smaller of the two energies). Now turn on a pertubation H ! , with the following matrix elements: # ...
... Suppose you’re given a quantum system whose Hamiltonian H0 admits two eigenstates, ψa (with energy Ea ), and ψb (with energy Eb ). They are orthogonal, normalized, and non-degenerate (assume Ea is the smaller of the two energies). Now turn on a pertubation H ! , with the following matrix elements: # ...
Simulations of the angular dependence of the dipole
... The energy exchange among Rydberg atoms has garnered great interest both as a probe of fundamental quantum dynamics and as a potential way to model other physical systems. The strong dipolar interactions among Rydberg atoms can block all but one excitation in a group of atoms, leading to a collectiv ...
... The energy exchange among Rydberg atoms has garnered great interest both as a probe of fundamental quantum dynamics and as a potential way to model other physical systems. The strong dipolar interactions among Rydberg atoms can block all but one excitation in a group of atoms, leading to a collectiv ...
Optical and Magnetic Properties of Copper(II) compounds.
... restrictions defining the pairs of energy levels between which such transitions can occur are called electron dipole selection rules.29 These rules, which can be explained in terms of symmetry of the wave-functions, are true only in the first approximation. The forbidden transitions are often observed ...
... restrictions defining the pairs of energy levels between which such transitions can occur are called electron dipole selection rules.29 These rules, which can be explained in terms of symmetry of the wave-functions, are true only in the first approximation. The forbidden transitions are often observed ...
Non-exponential and oscillatory decays in quantum mechanics
... The amplitudes Ac1 ≡ hc, E|H|1i are the matrix elements of the original Hamiltonian between an intrinsic state |1i and the channel state |c, Ei. The channel state is labeled here by the asymptotic energy E and all additional quantum numbers are combined in label c. For convenience, in this formalism ...
... The amplitudes Ac1 ≡ hc, E|H|1i are the matrix elements of the original Hamiltonian between an intrinsic state |1i and the channel state |c, Ei. The channel state is labeled here by the asymptotic energy E and all additional quantum numbers are combined in label c. For convenience, in this formalism ...
Charged domain walls as quantum strings on a - Instituut
... longer strictly obeyed when the density of topological defects is finite, it has been shown in a number of cases that they nevertheless remain genuine ultraviolet quantities as long as they do not overlap too strongly.31,32 If we consider a ~locally! directed piece of string, the string is analogous ...
... longer strictly obeyed when the density of topological defects is finite, it has been shown in a number of cases that they nevertheless remain genuine ultraviolet quantities as long as they do not overlap too strongly.31,32 If we consider a ~locally! directed piece of string, the string is analogous ...
The Quantum Phases of Matter The Harvard community has made
... flavors of many-body quantum entanglement. I will organize the discussion by classifying the states by the nature of their excitation spectrum. Readers interested primarily in strange metals can skip ahead to Section 4. First, in Section 2, I will consider phases in which there is a gap to all excit ...
... flavors of many-body quantum entanglement. I will organize the discussion by classifying the states by the nature of their excitation spectrum. Readers interested primarily in strange metals can skip ahead to Section 4. First, in Section 2, I will consider phases in which there is a gap to all excit ...
The Vacuum-Lattice model – a new route to longitudinal
... combined energy, 2mec2. The electrostatic component of the electron and positron mass is also almost entirely lost in the annihilation event because the negative and positive charge elements are rearranged into an alternating pattern in the vacuum lattice. To show this we can calculate the electrost ...
... combined energy, 2mec2. The electrostatic component of the electron and positron mass is also almost entirely lost in the annihilation event because the negative and positive charge elements are rearranged into an alternating pattern in the vacuum lattice. To show this we can calculate the electrost ...
Presentation slides
... “Count” to get two point correlation function analytically Fourier transform to give dynamical structure factor S(k, ω) Throughout we use units with ~ = kB = 1 ...
... “Count” to get two point correlation function analytically Fourier transform to give dynamical structure factor S(k, ω) Throughout we use units with ~ = kB = 1 ...
Chapter 2. Electronic, Vibrational and Spin
... visualize the electron configurations, the nuclear configurations and spin configurations of R, *R, I and P of Sch. 2.1. Next, we will describe some how to use these approximate wavefunctions to estimate some properties of R, *R, I and P through the use of Eq. 2.3. In these cases, in addition to vis ...
... visualize the electron configurations, the nuclear configurations and spin configurations of R, *R, I and P of Sch. 2.1. Next, we will describe some how to use these approximate wavefunctions to estimate some properties of R, *R, I and P through the use of Eq. 2.3. In these cases, in addition to vis ...
Temporal decay of Neel order in the one
... a state with perfect Néel order, the staggered magnetization is expected to decay to zero under the unitary time evolution with a SU(2)-symmetric Hamiltonian. This problem has been intensely studied for the spin-1/2 XXZ chain [6–14] and one observes a temporal power-law decay of the staggered magne ...
... a state with perfect Néel order, the staggered magnetization is expected to decay to zero under the unitary time evolution with a SU(2)-symmetric Hamiltonian. This problem has been intensely studied for the spin-1/2 XXZ chain [6–14] and one observes a temporal power-law decay of the staggered magne ...
Rotational Spectroscopy of Diatomic Molecules - Assets
... of intramolecular dynamic motion primarily involved. Historically the first method has been the most common, with different regions of the electromagnetic spectrum classified as shown in figure 1.1. In the figure we show four different ways of describing these regions. They may be classified accordi ...
... of intramolecular dynamic motion primarily involved. Historically the first method has been the most common, with different regions of the electromagnetic spectrum classified as shown in figure 1.1. In the figure we show four different ways of describing these regions. They may be classified accordi ...
The quantum phases of matter - Subir Sachdev
... flavors of many-body quantum entanglement. I will organize the discussion by classifying the states by the nature of their excitation spectrum. Readers interested primarily in strange metals can skip ahead to Section 4. First, in Section 2, I will consider phases in which there is a gap to all excit ...
... flavors of many-body quantum entanglement. I will organize the discussion by classifying the states by the nature of their excitation spectrum. Readers interested primarily in strange metals can skip ahead to Section 4. First, in Section 2, I will consider phases in which there is a gap to all excit ...
Physical systems for the solution of hard computational problems
... Figure 1.1: Likely structure of the NP problem class, taken from [58]. given NP-complete type in polynomial time, we could use this to solve any NPclass problem in polynomial time. For us, it means that we can focus on the task of designing a physical system to solve a particular NP-complete problem ...
... Figure 1.1: Likely structure of the NP problem class, taken from [58]. given NP-complete type in polynomial time, we could use this to solve any NPclass problem in polynomial time. For us, it means that we can focus on the task of designing a physical system to solve a particular NP-complete problem ...
On Exotic Orders in Stongly Correlated Systems
... the highly frustrated pyrochlore antiferromagnet. We find the energetically favored symmetric spin liquid state using a large Nf expansion, and present arguments for its stability to fluctuations about the infinite Nf mean-field state. Chapter 4 explains ...
... the highly frustrated pyrochlore antiferromagnet. We find the energetically favored symmetric spin liquid state using a large Nf expansion, and present arguments for its stability to fluctuations about the infinite Nf mean-field state. Chapter 4 explains ...
Questions from past exam papers. 1. (a) (8 marks) The Hamiltonian
... (ii) Interpret this result by developing the analogy between classical and quantum mechanics. (b) (6 marks) A quantum system can exist in two states |0i and |1i, which are normalised eigenstates of an observable A with eigenvalues 0 and 1 respectively. (Â has only these two eigenvalues). The quantu ...
... (ii) Interpret this result by developing the analogy between classical and quantum mechanics. (b) (6 marks) A quantum system can exist in two states |0i and |1i, which are normalised eigenstates of an observable A with eigenvalues 0 and 1 respectively. (Â has only these two eigenvalues). The quantu ...
Introduction to Integrable Models
... Colloquially, people often equate “Bethe-solvable” with “integrable”, but the set of integrable models is marginally bigger. The example with which we will start our journey is the one of a 1d ferromagnet. Here, one studies a linear chain of L identical atoms with only next-neighbor interactions. Ea ...
... Colloquially, people often equate “Bethe-solvable” with “integrable”, but the set of integrable models is marginally bigger. The example with which we will start our journey is the one of a 1d ferromagnet. Here, one studies a linear chain of L identical atoms with only next-neighbor interactions. Ea ...
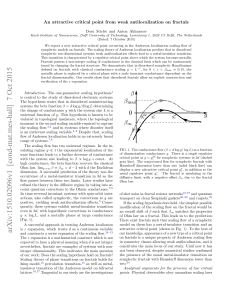
An attractive critical point from weak antilocalization on fractals
... exact value of β∞ for a Sierpiński gasket38 . For the classical 3 × 3 Sierpiński carpets, which lacks exact analytic results,39 we determine numerically β∞ ≈ −0.2, which lies within the bounds provided by the approximate renormalization group analysis.40–42 This result also means that classical Si ...
... exact value of β∞ for a Sierpiński gasket38 . For the classical 3 × 3 Sierpiński carpets, which lacks exact analytic results,39 we determine numerically β∞ ≈ −0.2, which lies within the bounds provided by the approximate renormalization group analysis.40–42 This result also means that classical Si ...
Detecting a many-body mobility edge with quantum
... the antiferromagnetic XXZ model in a random field [6, 7, 16, 17, 20], and the random-bond Ising model in a transverse field [19], among others. These models have the common feature that, when not protected from disorder by an energy gap, the ground state is localized for any arbitrary disorder stren ...
... the antiferromagnetic XXZ model in a random field [6, 7, 16, 17, 20], and the random-bond Ising model in a transverse field [19], among others. These models have the common feature that, when not protected from disorder by an energy gap, the ground state is localized for any arbitrary disorder stren ...