Lecture 15: The Hydrogen Atom
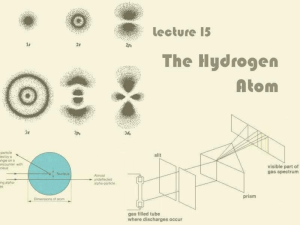
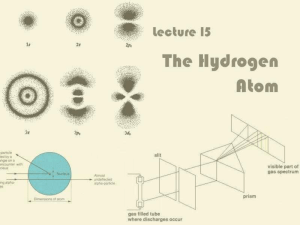
... Balmer’s Formula for Hydrogen Notice there are four bright lines in the hydrogen ...
... Balmer’s Formula for Hydrogen Notice there are four bright lines in the hydrogen ...
Final Exam Review
... 43. What is in the nucleus of an atom? 44. Write the orbital diagram & electron configurations for the following elements: K, Ar, H, He, Br 45. Define precision and accuracy. 46. What determines an element’s order on the periodic table? 47. What happens to the temperature of a substance as it is cha ...
... 43. What is in the nucleus of an atom? 44. Write the orbital diagram & electron configurations for the following elements: K, Ar, H, He, Br 45. Define precision and accuracy. 46. What determines an element’s order on the periodic table? 47. What happens to the temperature of a substance as it is cha ...
Document
... 44. Find the uncertainty relation between , the rotation angle about the z-axis, and Lz, the z component of the angular momentum. 45. A particle is in a potential V(x)=V0sin( 2x / a ), which is invariant under the transformation x→x+ma, where m is an integer. Is momentum conserved? Discuss the ei ...
... 44. Find the uncertainty relation between , the rotation angle about the z-axis, and Lz, the z component of the angular momentum. 45. A particle is in a potential V(x)=V0sin( 2x / a ), which is invariant under the transformation x→x+ma, where m is an integer. Is momentum conserved? Discuss the ei ...
2·QUIZLET VOCABULARY: Quantum Numbers Study online at
... 4. Hunds rule: orbitals of equal energy are each occupied by one electron before any orbital is occupied by a second electron, and all electrons in singly occupied orbitals must have the same spin 5. Magnetic (orbital) quantum Number: ml Indicates orientation of orbital in space S- 1 orbital P- 3 or ...
... 4. Hunds rule: orbitals of equal energy are each occupied by one electron before any orbital is occupied by a second electron, and all electrons in singly occupied orbitals must have the same spin 5. Magnetic (orbital) quantum Number: ml Indicates orientation of orbital in space S- 1 orbital P- 3 or ...
ChemicalBondingTestAnswers
... 4. In beaker (B) - Dipole-dipole forces act between molecules possessing permanent dipoles. Ends of dipoles possess partial positive and negative charges which account for electrostatic forces of attraction and hence dipole-dipole forces. We can guess that if a molecule is polar then mostly it is bo ...
... 4. In beaker (B) - Dipole-dipole forces act between molecules possessing permanent dipoles. Ends of dipoles possess partial positive and negative charges which account for electrostatic forces of attraction and hence dipole-dipole forces. We can guess that if a molecule is polar then mostly it is bo ...
Lecture 15: The Hydrogen Atom
... For historical reasons, ℓ = 0, 1, 2, 3 is also known as s, p, d, f ...
... For historical reasons, ℓ = 0, 1, 2, 3 is also known as s, p, d, f ...
2.5 Bohr Model and Electron Energy
... 1. Electrons travel in set paths around the nucleus called orbits or energy levels. 2. Each orbit corresponds with an energy level. a. Electrons have a natural tendency to occupy the lowest (most stable) energy level first. i. The lowest energy level (ground state) is the closest to the nucleus. ...
... 1. Electrons travel in set paths around the nucleus called orbits or energy levels. 2. Each orbit corresponds with an energy level. a. Electrons have a natural tendency to occupy the lowest (most stable) energy level first. i. The lowest energy level (ground state) is the closest to the nucleus. ...
Chapter 7, 8, and 9 Exam 2014 Name I. 50% of your grade will come
... Chapter 7, 8, and 9 Exam 2016 ...
... Chapter 7, 8, and 9 Exam 2016 ...
B - Piazza
... molecules—the positive and negative charges both behave like point sources and so their fields cancel out perfectly! So how do molecules form? ...
... molecules—the positive and negative charges both behave like point sources and so their fields cancel out perfectly! So how do molecules form? ...
chapter-27-1-with
... Max Planck found he could explain these curves if he assumed that electromagnetic energy was radiated in ...
... Max Planck found he could explain these curves if he assumed that electromagnetic energy was radiated in ...
Ch4 notes - Midway ISD
... • Unique to each element, used for identification • Continuous spectrum ...
... • Unique to each element, used for identification • Continuous spectrum ...