Chapter 2 Chemistry comes alive
... the nucleus of an atom Bonds are formed using the electrons in the outermost energy level Valence shell – outermost energy level containing chemically active electrons Octet rule – except for the first shell which is full with two electrons, atoms interact in a manner to have eight electrons in thei ...
... the nucleus of an atom Bonds are formed using the electrons in the outermost energy level Valence shell – outermost energy level containing chemically active electrons Octet rule – except for the first shell which is full with two electrons, atoms interact in a manner to have eight electrons in thei ...
Name: Date: Period: Who is the Father of Atomic Theory? What
... 13. Circle the correct answers. “The mass of the products (always / sometimes / never) equals the mass of the reactants. This statement summarizes the Law of Conservation of (mass / energy).” 14. How are the following terms related: mole, formula mass, and atomic mass units? ...
... 13. Circle the correct answers. “The mass of the products (always / sometimes / never) equals the mass of the reactants. This statement summarizes the Law of Conservation of (mass / energy).” 14. How are the following terms related: mole, formula mass, and atomic mass units? ...
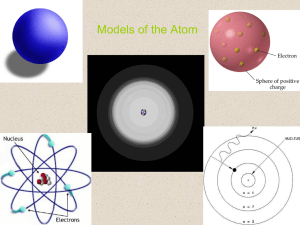
Atomic models: nuclear to quantum
... velocity would slow, and they would spiral into the nucleus and collapse the atom. But, in the subatomic quantum world, atoms are subject to quantum mechanics rather than the Newtonian laws of motion. • Electrons have quantum energy and that level of energy can only be changed transiently. • Uncerta ...
... velocity would slow, and they would spiral into the nucleus and collapse the atom. But, in the subatomic quantum world, atoms are subject to quantum mechanics rather than the Newtonian laws of motion. • Electrons have quantum energy and that level of energy can only be changed transiently. • Uncerta ...
Quantum Factorization of 143 on a Dipolar
... and set each factor’s first bit (i.e., most significant bit) to be 1. In a realistic problem, the width of p or q could not be known a priori. Thus one need to verify the answer (i.e., pq ¼ N, which cost polynomial time) of each try until the solution is found. Note that these tries will not increas ...
... and set each factor’s first bit (i.e., most significant bit) to be 1. In a realistic problem, the width of p or q could not be known a priori. Thus one need to verify the answer (i.e., pq ¼ N, which cost polynomial time) of each try until the solution is found. Note that these tries will not increas ...
Lecture 5 - Ultra high energy cosmic rays and the GZK cutoff
... given the symbol s. It’s an invariant quantity. Furthermore, because total energy and total momentum are conserved, it’s also a conserved quantity when calculated before and after some collision or decay. Note that the above does not mean that any system of particles is equivalent to a set of partic ...
... given the symbol s. It’s an invariant quantity. Furthermore, because total energy and total momentum are conserved, it’s also a conserved quantity when calculated before and after some collision or decay. Note that the above does not mean that any system of particles is equivalent to a set of partic ...
Variational principle in the conservation operators deduction
... In connection with the latter it is interesting to consider another one feature of the deduction: the obtained operators (56) are the quanta operators but, however, there is no one explicit quantum term in the starting equations 4,7,8. Quantum term A is emerged on the step (35) as a result of bound ...
... In connection with the latter it is interesting to consider another one feature of the deduction: the obtained operators (56) are the quanta operators but, however, there is no one explicit quantum term in the starting equations 4,7,8. Quantum term A is emerged on the step (35) as a result of bound ...
ppt
... POSITION AND SPEED OF ELECTRON AT A GIVEN TIME At best, we can describe the probability of finding it at a specific place ...
... POSITION AND SPEED OF ELECTRON AT A GIVEN TIME At best, we can describe the probability of finding it at a specific place ...
Creating Entanglement
... The Hamiltonian The Hamiltonian operator is a function of operators concerning degrees of freedom (dynamical variables) of the system. Eg. if quantum information is encoded in positions x1 and x2 of two particles, then with … representing other relevant operators. Momentum p is conjugate to p ...
... The Hamiltonian The Hamiltonian operator is a function of operators concerning degrees of freedom (dynamical variables) of the system. Eg. if quantum information is encoded in positions x1 and x2 of two particles, then with … representing other relevant operators. Momentum p is conjugate to p ...
NAME PRACTICE: QUANTUM CONFIGURATIONS 1) Each of the
... ___12) Helium, 42He, has two electrons in the 1s orbital. When it becomes ionized, forming He+, ...
... ___12) Helium, 42He, has two electrons in the 1s orbital. When it becomes ionized, forming He+, ...
Exact solutions of effective
... general form of the effective-mass Hamiltonian without any restriction in the ordering parameters, for a system with smooth potential and mass step. The effective mass Hamiltonian and the connection rules for a system with abrupt heterojunction were deduced from the study of the limiting case when t ...
... general form of the effective-mass Hamiltonian without any restriction in the ordering parameters, for a system with smooth potential and mass step. The effective mass Hamiltonian and the connection rules for a system with abrupt heterojunction were deduced from the study of the limiting case when t ...