Quantum Nonlinear Resonances in Atom Optics
... Definition of a temperature for this system? Measurement of the thermodynamic function? ...
... Definition of a temperature for this system? Measurement of the thermodynamic function? ...
The rotating frame
... the second condition. The first condition can also be satisfied if we assume hθ = Lθ = r for all r. Solving for hz and hr To determine hr imagine the following: An observer is at rest in a rotating frame a distance r from its axis. Another observer is in an inertial frame and determines the first ob ...
... the second condition. The first condition can also be satisfied if we assume hθ = Lθ = r for all r. Solving for hz and hr To determine hr imagine the following: An observer is at rest in a rotating frame a distance r from its axis. Another observer is in an inertial frame and determines the first ob ...
Lecture 8 Relevant sections in text: §1.6 Momentum
... In fact, the self-adjointness of P is also sufficient for T to be unitary. This can be seen by representing Ta as an infinite product of infinitesimal transformations: Ta = lim (I − N →∞ ...
... In fact, the self-adjointness of P is also sufficient for T to be unitary. This can be seen by representing Ta as an infinite product of infinitesimal transformations: Ta = lim (I − N →∞ ...
Part II. Statistical mechanics Chapter 9. Classical and quantum
... imposed constraints; e.g. ρeq (qi , pi ,U,V ) is the set of all possible system trajectories such that U and V are constant. The more general goal of non-equilibrium statistical mechanics is to find A(t) given an initial condition ρ0 (qi , pi ; constraints) . So much for the classical picture. ...
... imposed constraints; e.g. ρeq (qi , pi ,U,V ) is the set of all possible system trajectories such that U and V are constant. The more general goal of non-equilibrium statistical mechanics is to find A(t) given an initial condition ρ0 (qi , pi ; constraints) . So much for the classical picture. ...
Electrons in Atoms
... numbers (n, l , ml) and the nomenclature s, p, d, f etc Relate properties of atomic orbitals (e.g. energy, shape, directional) to the quantum numbers n, l , ml Determine permitted values for l and ml for a given value of n Sketch the shapes (boundary surfaces) of s, 2p and 3d-orbitals with ref ...
... numbers (n, l , ml) and the nomenclature s, p, d, f etc Relate properties of atomic orbitals (e.g. energy, shape, directional) to the quantum numbers n, l , ml Determine permitted values for l and ml for a given value of n Sketch the shapes (boundary surfaces) of s, 2p and 3d-orbitals with ref ...
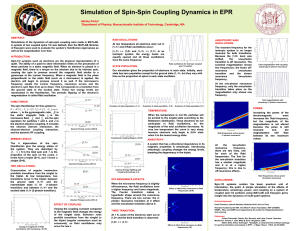
Simulation of Spin-Spin Coupling Dynamics in EPR
... these particles in a static magnetic field. When an electron is placed in a magnetic field, there is a torque on the electron due to its intrinsic intrinsic spin, causing the spin to precess around the magnetic field similar to a gyroscope at the Larmor frequency. When a magnetic field in the plane ...
... these particles in a static magnetic field. When an electron is placed in a magnetic field, there is a torque on the electron due to its intrinsic intrinsic spin, causing the spin to precess around the magnetic field similar to a gyroscope at the Larmor frequency. When a magnetic field in the plane ...
vander waals forces in an inhomogeneous dielectric
... Here, evidently, fluctuations with wavelengths of the order of the dimensions of the inhomogeneities are significant (for example, of the order of the film thickness or of the distance between the attracting solids). This makes possible a macroscopic analysis for macroscopic bodies and to express th ...
... Here, evidently, fluctuations with wavelengths of the order of the dimensions of the inhomogeneities are significant (for example, of the order of the film thickness or of the distance between the attracting solids). This makes possible a macroscopic analysis for macroscopic bodies and to express th ...
CH 4 SEC 2: Book Notes
... w Values of the principle quantum number are positive integers only—1, 2, 3, and so on. (principle quantum number is referred as n) w As n increases, the electron’s energy and its average distance from the nucleus increase. (see Figure 12) w more than one electron can have the same n value. These ...
... w Values of the principle quantum number are positive integers only—1, 2, 3, and so on. (principle quantum number is referred as n) w As n increases, the electron’s energy and its average distance from the nucleus increase. (see Figure 12) w more than one electron can have the same n value. These ...
Electrons as waves
... Schrodinger’s equation laid the foundation for quantum theory. • Quantum theory- describes mathematically the wave properties of electrons and other very small particles. ...
... Schrodinger’s equation laid the foundation for quantum theory. • Quantum theory- describes mathematically the wave properties of electrons and other very small particles. ...
CHAPTER 9: Statistical Physics
... energy and jump to a higher state. Therefore the fraction of electrons capable of participating in this thermal process is on the order of kT / EF. ...
... energy and jump to a higher state. Therefore the fraction of electrons capable of participating in this thermal process is on the order of kT / EF. ...
honors chem 6 day review packet
... Potassium Sulfur Cobalt P−3 Mg+2 Valence electrons are electrons in the outer shell. Draw the dot diagrams for the following: Potassium ...
... Potassium Sulfur Cobalt P−3 Mg+2 Valence electrons are electrons in the outer shell. Draw the dot diagrams for the following: Potassium ...