PHY492: Nuclear & Particle Physics Lecture 4 Nature of the nuclear force
... Obtain Rutherford scattering via quantum mechanics Assume: ...
... Obtain Rutherford scattering via quantum mechanics Assume: ...
Day 4 - Academic Computer Center
... would all interact with all the gold atoms in about the same way. But what he found was that most of the bullets went straight through, although some of them were bent as though they had hit something hard. He theorized that some of the sub-atomic particles were clustered in the center of the atom a ...
... would all interact with all the gold atoms in about the same way. But what he found was that most of the bullets went straight through, although some of them were bent as though they had hit something hard. He theorized that some of the sub-atomic particles were clustered in the center of the atom a ...
URL - StealthSkater
... It just happens to turn out that when we use Niobium (which is a superconductor) with the temperatures of outer space on our hull … It turns out if you put electrons on Niobium … Well, the electrons line up in this triangular array where they’re all at a certain distance one from another. That dista ...
... It just happens to turn out that when we use Niobium (which is a superconductor) with the temperatures of outer space on our hull … It turns out if you put electrons on Niobium … Well, the electrons line up in this triangular array where they’re all at a certain distance one from another. That dista ...
Lecture Outline - Mechanical and Industrial Engineering
... • length [ft], time [s], force [lb, lbf] • mass is derived [m=W/g, 32.2 lb/ 32.2 ft/s2 = 1.0 slug] ...
... • length [ft], time [s], force [lb, lbf] • mass is derived [m=W/g, 32.2 lb/ 32.2 ft/s2 = 1.0 slug] ...
steady state solution
... Know the definitions of power (or rate of work) of a force, and work done by a force Know the definition of kinetic energy of a particle Understand power-work-kinetic energy relations for a particle Be able to use work/power/kinetic energy to solve problems involving particle motion Be able to disti ...
... Know the definitions of power (or rate of work) of a force, and work done by a force Know the definition of kinetic energy of a particle Understand power-work-kinetic energy relations for a particle Be able to use work/power/kinetic energy to solve problems involving particle motion Be able to disti ...
ppt
... Before going on: Remember that this all boils down to particles Mass, position, velocity, (linear) momentum, force are fundamental Inertia tensor, orientation, angular velocity, angular momentum, torque are just abstractions Don’t get too puzzled about interpretation of torque for example: ...
... Before going on: Remember that this all boils down to particles Mass, position, velocity, (linear) momentum, force are fundamental Inertia tensor, orientation, angular velocity, angular momentum, torque are just abstractions Don’t get too puzzled about interpretation of torque for example: ...
2 - Physics at Oregon State University
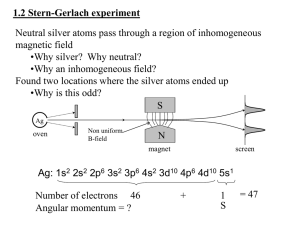
... •How can a neutral atom interact with a magnetic field? •Let’s derive it classically from intro-course principles •What does a simple magnetic dipole look like? •What does the energy look like? •What will the force be and why does the B need to be inhomogeneous? •How do we relate this to angular mom ...
... •How can a neutral atom interact with a magnetic field? •Let’s derive it classically from intro-course principles •What does a simple magnetic dipole look like? •What does the energy look like? •What will the force be and why does the B need to be inhomogeneous? •How do we relate this to angular mom ...
Chapter 48 Nuclear Structure (Examples) (SM13) Example 1: What
... Example 1: What is the ratio of the density of a proton to the density of a U 238 nucleus? Example 2: What is the acceleration due to gravity at the surface of a neutron star if its radius is 10 km? Example 3: Calculate the binding energy per nucleon for He 4. H 1 mass = 1.007825 u n mass = 1.008665 ...
... Example 1: What is the ratio of the density of a proton to the density of a U 238 nucleus? Example 2: What is the acceleration due to gravity at the surface of a neutron star if its radius is 10 km? Example 3: Calculate the binding energy per nucleon for He 4. H 1 mass = 1.007825 u n mass = 1.008665 ...
Particle Accelerators - Stony Brook University
... What can we accelerate? All accelerators are based on acceleration of charged particles by electric forces. Electric field E Force F = q E proton of charge q We accelerate elementary particles and nuclei which have small mass (F = ma, so a = F/m) to get beams of high velocity (and energy). Bringing ...
... What can we accelerate? All accelerators are based on acceleration of charged particles by electric forces. Electric field E Force F = q E proton of charge q We accelerate elementary particles and nuclei which have small mass (F = ma, so a = F/m) to get beams of high velocity (and energy). Bringing ...
Electrostatics pset
... 2. What is the magnitude of the electric force of attraction between an iron nucleus (q = +26e) and its innermost electron if the distance between them is 1.5×10–12 m? 3. What is the magnitude of the force a +25 μC charge exerts on a +2.5 mC charge 16 cm away? 4. What is the repulsive electrical for ...
... 2. What is the magnitude of the electric force of attraction between an iron nucleus (q = +26e) and its innermost electron if the distance between them is 1.5×10–12 m? 3. What is the magnitude of the force a +25 μC charge exerts on a +2.5 mC charge 16 cm away? 4. What is the repulsive electrical for ...
Structure of Atom
... They are positively charged particles with mass 1.67262 × 10–27 kg & charge equal to 1.6022 × 10–19C. Proton was discovered by Goldstein (1866). They are present in highly dense central part of atom called nucleus of atom. Their mass is 1.007274. They are . Neutron : It is neutral particle with mas ...
... They are positively charged particles with mass 1.67262 × 10–27 kg & charge equal to 1.6022 × 10–19C. Proton was discovered by Goldstein (1866). They are present in highly dense central part of atom called nucleus of atom. Their mass is 1.007274. They are . Neutron : It is neutral particle with mas ...
Слайд 1 - QUARKS
... • Lorentzian Wormhole is a region in spacetime in which 3-dim space-like sections have non-trivial topology. • By non-trivial topology we mean that these sections are not simply connected • In the simplest case a WH has two mouths which join different regions of the space-time. • We can also imagine ...
... • Lorentzian Wormhole is a region in spacetime in which 3-dim space-like sections have non-trivial topology. • By non-trivial topology we mean that these sections are not simply connected • In the simplest case a WH has two mouths which join different regions of the space-time. • We can also imagine ...
CHM1045 - Michael Blaber
... * = c (the relationship between wavelength, frequency and speed of light for electromagnetic radiation) E = h * (the relationship between energy and frequency for electromagnetic radiation En = -RH / n2 or En = -B / n2 (the relationship between the energy of an electron in Bohr's model of the ...
... * = c (the relationship between wavelength, frequency and speed of light for electromagnetic radiation) E = h * (the relationship between energy and frequency for electromagnetic radiation En = -RH / n2 or En = -B / n2 (the relationship between the energy of an electron in Bohr's model of the ...
PPT
... simplicity, we say it doesn't exist. If we say that precise x and p simultaneously exist (at least in the usual meaning of those words) we will directly run into predictions which violate both QM and experience, since interference is found between parts of the wave at different x's and p's, leaving ...
... simplicity, we say it doesn't exist. If we say that precise x and p simultaneously exist (at least in the usual meaning of those words) we will directly run into predictions which violate both QM and experience, since interference is found between parts of the wave at different x's and p's, leaving ...
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle whose substructure is unknown, thus it is unknown whether it is composed of other particles. Known elementary particles include the fundamental fermions (quarks, leptons, antiquarks, and antileptons), which generally are ""matter particles"" and ""antimatter particles"", as well as the fundamental bosons (gauge bosons and Higgs boson), which generally are ""force particles"" that mediate interactions among fermions. A particle containing two or more elementary particles is a composite particle.Everyday matter is composed of atoms, once presumed to be matter's elementary particles—atom meaning ""indivisible"" in Greek—although the atom's existence remained controversial until about 1910, as some leading physicists regarded molecules as mathematical illusions, and matter as ultimately composed of energy. Soon, subatomic constituents of the atom were identified. As the 1930s opened, the electron and the proton had been observed, along with the photon, the particle of electromagnetic radiation. At that time, the recent advent of quantum mechanics was radically altering the conception of particles, as a single particle could seemingly span a field as would a wave, a paradox still eluding satisfactory explanation.Via quantum theory, protons and neutrons were found to contain quarks—up quarks and down quarks—now considered elementary particles. And within a molecule, the electron's three degrees of freedom (charge, spin, orbital) can separate via wavefunction into three quasiparticles (holon, spinon, orbiton). Yet a free electron—which, not orbiting an atomic nucleus, lacks orbital motion—appears unsplittable and remains regarded as an elementary particle.Around 1980, an elementary particle's status as indeed elementary—an ultimate constituent of substance—was mostly discarded for a more practical outlook, embodied in particle physics' Standard Model, science's most experimentally successful theory. Many elaborations upon and theories beyond the Standard Model, including the extremely popular supersymmetry, double the number of elementary particles by hypothesizing that each known particle associates with a ""shadow"" partner far more massive, although all such superpartners remain undiscovered. Meanwhile, an elementary boson mediating gravitation—the graviton—remains hypothetical.