Electric polarization properties of single bacteria measured with electrostatic force microscopy
... In Figure 8.5 shows the variation of the capacitance‐gradient contrast, C’(z, r, e), as a function of tip–nanoparticle distance, z, for the case of a solid oblate spheroid of dielectric constant r = 6.3, height D = 39 nm and eccentricities e = 1, 2, 5, 10 and 30 (for e > 30 ...
... In Figure 8.5 shows the variation of the capacitance‐gradient contrast, C’(z, r, e), as a function of tip–nanoparticle distance, z, for the case of a solid oblate spheroid of dielectric constant r = 6.3, height D = 39 nm and eccentricities e = 1, 2, 5, 10 and 30 (for e > 30 ...
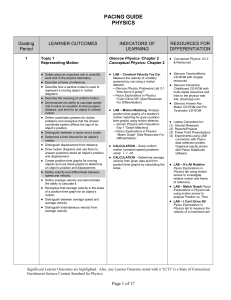
Pacing Guide for Physics
... cardboard students will draw an ellipse and use it to explain Kepler’s laws. ---Glencoe Physics Text Lab (Pages 186-187) “Modeling the Orbits of Planets and Satellites” ...
... cardboard students will draw an ellipse and use it to explain Kepler’s laws. ---Glencoe Physics Text Lab (Pages 186-187) “Modeling the Orbits of Planets and Satellites” ...
chapter 3 part 1
... can alter an objects speed, its direction, or both. • All forces have a strength (magnitude) and a direction. Therefore • , forces are vector quantities. ...
... can alter an objects speed, its direction, or both. • All forces have a strength (magnitude) and a direction. Therefore • , forces are vector quantities. ...
Instituto Nacional de Astrofísica, Optica y Electrónica.
... radiation force that enables to control the position of objects and possibly deform them. On the other hand, the transfer of angular momentum results in a radiation torque that can be used to rotate material systems. Mechanical effects of waves on material media is a powerful option to achieve conta ...
... radiation force that enables to control the position of objects and possibly deform them. On the other hand, the transfer of angular momentum results in a radiation torque that can be used to rotate material systems. Mechanical effects of waves on material media is a powerful option to achieve conta ...
Vibration Dynamics
... in which, x is a column array of describing coordinates of the system, and f is a column array of the associated applied forces. The square matrices [m], [c], [k] are the mass, damping, and stiffness matrices. Example 30 (The one, two, and three DOF model of vehicles) The one, two, and three DOF mod ...
... in which, x is a column array of describing coordinates of the system, and f is a column array of the associated applied forces. The square matrices [m], [c], [k] are the mass, damping, and stiffness matrices. Example 30 (The one, two, and three DOF model of vehicles) The one, two, and three DOF mod ...
GCE Physics B: Physics in Context Teacher Resource Bank
... The Moon’s orbit around the Earth may be assumed to be circular. Explain why no work is done by the gravitational force that acts on the Moon to keep it in orbit around the Earth. You may be awarded marks for the quality of written communication provided in your answer. ...
... The Moon’s orbit around the Earth may be assumed to be circular. Explain why no work is done by the gravitational force that acts on the Moon to keep it in orbit around the Earth. You may be awarded marks for the quality of written communication provided in your answer. ...
Ch#6 - KFUPM Faculty List
... Q20: A block of mass m = 10 kg is pushed up a rough 30 o inclined plane by a force F parallel to the incline as shown in Figure 4. The coefficient of kinetic friction between the block and the plane is 0.4. Find the magnitude of the force F when the block is moving up at constant velocity. (Ans: 83 ...
... Q20: A block of mass m = 10 kg is pushed up a rough 30 o inclined plane by a force F parallel to the incline as shown in Figure 4. The coefficient of kinetic friction between the block and the plane is 0.4. Find the magnitude of the force F when the block is moving up at constant velocity. (Ans: 83 ...
Sample Papers 1 - Entrance
... in its volume, the normal force per unit area is called bulk stress or volume stress. 13. Bulk stress is equal to pressure or change in pressure also called hydraulic pressure. 14. Shearing stress or Tangential stress : When a tangential force is applied on a body such that there is a change in shap ...
... in its volume, the normal force per unit area is called bulk stress or volume stress. 13. Bulk stress is equal to pressure or change in pressure also called hydraulic pressure. 14. Shearing stress or Tangential stress : When a tangential force is applied on a body such that there is a change in shap ...
Linear Momentum and Collisions
... In Chapter 8, we studied situations that are difficult to analyze with Newton’s laws. We were able to solve problems involving these situations by identifying a system and applying a conservation principle, conservation of energy. Let us consider another situation and see if we can solve it with the ...
... In Chapter 8, we studied situations that are difficult to analyze with Newton’s laws. We were able to solve problems involving these situations by identifying a system and applying a conservation principle, conservation of energy. Let us consider another situation and see if we can solve it with the ...
Final Newtons Review
... b. If a football is moving upwards and rightwards towards the peak of its trajectory, then there are both rightwards and upwards forces acting upon it. c. It would take an unbalanced force to keep an object in motion. d. If an object is at rest, then there are no forces acting upon the object. e. It ...
... b. If a football is moving upwards and rightwards towards the peak of its trajectory, then there are both rightwards and upwards forces acting upon it. c. It would take an unbalanced force to keep an object in motion. d. If an object is at rest, then there are no forces acting upon the object. e. It ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.