Momentum - Sackville School
... Mass is measured in kilograms (kg). Velocity is measured in metres per second (m/s). Momentum is measured in kilogram metres per second (kg m/s). ...
... Mass is measured in kilograms (kg). Velocity is measured in metres per second (m/s). Momentum is measured in kilogram metres per second (kg m/s). ...
Advancing Physics A2
... It is not difficult to illustrate this principle with a very bright small light source, a screen and a square hole at the centre of a thick card. Start with the screen just behind the ‘hole’. With the ‘hole’ fixed in position, the same light is spread over four times the area when the distance betwe ...
... It is not difficult to illustrate this principle with a very bright small light source, a screen and a square hole at the centre of a thick card. Start with the screen just behind the ‘hole’. With the ‘hole’ fixed in position, the same light is spread over four times the area when the distance betwe ...
DYNAMICS AND RELATIVITY (PART II)
... Where does this energy come from? The higher the object is at the start, the more potential it has to gain energy when it falls. We say that an object of mass m, at a height y, has gravitational potential energy, given by Notice that it doesn’t really matter where the point y = 0 is, since only chan ...
... Where does this energy come from? The higher the object is at the start, the more potential it has to gain energy when it falls. We say that an object of mass m, at a height y, has gravitational potential energy, given by Notice that it doesn’t really matter where the point y = 0 is, since only chan ...
Chapter 20 Lecture Notes 2011
... Vector Sum of Electrical Forces Steps: 1. Find the force exerted between individual bodies using Coulomb’s Law. 2. Use the charge to define the direction. 3. Find the x and y components. 4. Add up the total x and y force component 5. Use the Pythagoream Theorum to find the resultant. 6. Use tan to ...
... Vector Sum of Electrical Forces Steps: 1. Find the force exerted between individual bodies using Coulomb’s Law. 2. Use the charge to define the direction. 3. Find the x and y components. 4. Add up the total x and y force component 5. Use the Pythagoream Theorum to find the resultant. 6. Use tan to ...
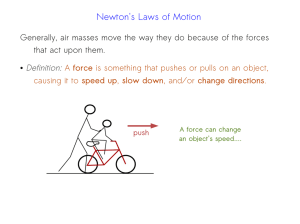
Newton`s Laws of Motion
... So the key to understanding atmospheric motions is to understand the forces that produce these motions. And what, pray tell, are these forces you speak of? Well, for our purposes, the main ones are: (i) the pressure gradient force (PGF) (ii) the Coriolis force ...
... So the key to understanding atmospheric motions is to understand the forces that produce these motions. And what, pray tell, are these forces you speak of? Well, for our purposes, the main ones are: (i) the pressure gradient force (PGF) (ii) the Coriolis force ...
Extra Problem of Chapter 5 to 8 Question 1
... (C) W f = ! fk ( 4.5m ) = ! ( 85.9N ) ( 4.5m ) = !387J . Wf < 0 since the friction force is in the opposite direction of displacement. (D) The normal force and gravity is perpendicular to the direction of motion, so the work done by these forces are zero. (E) The total work done is WT = WA + W f = 3 ...
... (C) W f = ! fk ( 4.5m ) = ! ( 85.9N ) ( 4.5m ) = !387J . Wf < 0 since the friction force is in the opposite direction of displacement. (D) The normal force and gravity is perpendicular to the direction of motion, so the work done by these forces are zero. (E) The total work done is WT = WA + W f = 3 ...
Part A: Elevator Is At Rest.
... To the occupants of the downwardly accelerating elevator, it appears that gravity is weaker, since they seem to weigh less (why?) and objects fall more slowly than "normal." ...
... To the occupants of the downwardly accelerating elevator, it appears that gravity is weaker, since they seem to weigh less (why?) and objects fall more slowly than "normal." ...
Springs Practice Questions_PDF
... (1) If a force of 50 N is applied to a spring, by how much will that spring stretch if it has a spring constant, k, of 5 N/m? Suppose the same force is applied to another spring with a spring constant of 10 N/m, by how much will this spring stretch? (2) By how much will a spring compress if a 6.0 kg ...
... (1) If a force of 50 N is applied to a spring, by how much will that spring stretch if it has a spring constant, k, of 5 N/m? Suppose the same force is applied to another spring with a spring constant of 10 N/m, by how much will this spring stretch? (2) By how much will a spring compress if a 6.0 kg ...
Sample pages 2 PDF
... In Fig. 2.4, a simplified basic lift distribution for an aeroplane is given. The mass of the plane, including fuel and payload, is m = 45,200 kg. The following values are assumed for the widths bi of the sections: b1 = 1 m; b2 = 7 m; b3 = 3 m; b4 = 2 m, and for the corresponding basic lift forces: l ...
... In Fig. 2.4, a simplified basic lift distribution for an aeroplane is given. The mass of the plane, including fuel and payload, is m = 45,200 kg. The following values are assumed for the widths bi of the sections: b1 = 1 m; b2 = 7 m; b3 = 3 m; b4 = 2 m, and for the corresponding basic lift forces: l ...
s - Nuffield Foundation
... find the frictional force acting on each can. 4 A sledge has mass 15 kg. A horizontal pull of 25 N will just move the sledge when it is on a horizontal surface of compacted snow. a Draw a diagram showing the forces acting on the sledge, modelled as a particle, when it is just on the point of sliding ...
... find the frictional force acting on each can. 4 A sledge has mass 15 kg. A horizontal pull of 25 N will just move the sledge when it is on a horizontal surface of compacted snow. a Draw a diagram showing the forces acting on the sledge, modelled as a particle, when it is just on the point of sliding ...
Mass versus weight

In everyday usage, the mass of an object is often referred to as its weight though these are in fact different concepts and quantities. In scientific contexts, mass refers loosely to the amount of ""matter"" in an object (though ""matter"" may be difficult to define), whereas weight refers to the force experienced by an object due to gravity. In other words, an object with a mass of 1.0 kilogram will weigh approximately 9.81 newtons (newton is the unit of force, while kilogram is the unit of mass) on the surface of the Earth (its mass multiplied by the gravitational field strength). Its weight will be less on Mars (where gravity is weaker), more on Saturn, and negligible in space when far from any significant source of gravity, but it will always have the same mass.Objects on the surface of the Earth have weight, although sometimes this weight is difficult to measure. An example is a small object floating in a pool of water (or even on a dish of water), which does not appear to have weight since it is buoyed by the water; but it is found to have its usual weight when it is added to water in a container which is entirely supported by and weighed on a scale. Thus, the ""weightless object"" floating in water actually transfers its weight to the bottom of the container (where the pressure increases). Similarly, a balloon has mass but may appear to have no weight or even negative weight, due to buoyancy in air. However the weight of the balloon and the gas inside it has merely been transferred to a large area of the Earth's surface, making the weight difficult to measure. The weight of a flying airplane is similarly distributed to the ground, but does not disappear. If the airplane is in level flight, the same weight-force is distributed to the surface of the Earth as when the plane was on the runway, but spread over a larger area.A better scientific definition of mass is its description as being composed of inertia, which basically is the resistance of an object being accelerated when acted on by an external force. Gravitational ""weight"" is the force created when a mass is acted upon by a gravitational field and the object is not allowed to free-fall, but is supported or retarded by a mechanical force, such as the surface of a planet. Such a force constitutes weight. This force can be added to by any other kind of force.For example, in the photograph, the girl's weight, subtracted from the tension in the chain (respectively the support force of the seat), yields the necessary centripetal force to keep her swinging in an arc. If one stands behind her at the bottom of her arc and abruptly stops her, the impetus (""bump"" or stopping-force) one experiences is due to acting against her inertia, and would be the same even if gravity were suddenly switched off.While the weight of an object varies in proportion to the strength of the gravitational field, its mass is constant (ignoring relativistic effects) as long as no energy or matter is added to the object. Accordingly, for an astronaut on a spacewalk in orbit (a free-fall), no effort is required to hold a communications satellite in front of him; it is ""weightless"". However, since objects in orbit retain their mass and inertia, an astronaut must exert ten times as much force to accelerate a 10‑ton satellite at the same rate as one with a mass of only 1 ton.On Earth, a swing set can demonstrate this relationship between force, mass, and acceleration. If one were to stand behind a large adult sitting stationary on a swing and give him a strong push, the adult would temporarily accelerate to a quite low speed, and then swing only a short distance before beginning to swing in the opposite direction. Applying the same impetus to a small child would produce a much greater speed.