Electro Static - Career Launcher
... One dimensional equations of motion Distance s = area under v-t graph = ½ (u+v)t Using equation of motion (1) s = ut + ½ at2 Equation of motion (2) But, s = vavgt Hence, vavg = (u+v)/2 As t ...
... One dimensional equations of motion Distance s = area under v-t graph = ½ (u+v)t Using equation of motion (1) s = ut + ½ at2 Equation of motion (2) But, s = vavgt Hence, vavg = (u+v)/2 As t ...
mec65
... The net force acting on the particle can never be negative ( Fnet 0 ), so the maximum value of the resistive force is FR _ max m g . When the net force acting on the particle is zero (Fnet = 0), the acceleration must also be zero (a = 0), therefore the particle will move downward with a constant ...
... The net force acting on the particle can never be negative ( Fnet 0 ), so the maximum value of the resistive force is FR _ max m g . When the net force acting on the particle is zero (Fnet = 0), the acceleration must also be zero (a = 0), therefore the particle will move downward with a constant ...
Document
... interval t. The force is then removed and applied to object 2. After object 2 has accelerated for the same time interval t, which statements are true? a) b) c) d) e) f) ...
... interval t. The force is then removed and applied to object 2. After object 2 has accelerated for the same time interval t, which statements are true? a) b) c) d) e) f) ...
simple harmonic motion - IndiaStudyChannel.com
... The time taken for one complete vibration or oscillation is called time period (T). The number of oscillations or vibrations made per second is called frequency (n). The maximum displacement of a particle measured from the equilibrium position is called amplitude (A). Phase is defined as the ...
... The time taken for one complete vibration or oscillation is called time period (T). The number of oscillations or vibrations made per second is called frequency (n). The maximum displacement of a particle measured from the equilibrium position is called amplitude (A). Phase is defined as the ...
Unit 1 content
... Kinetic Theory of Gases • Gas exerts a pressure because the particles hit wall of container ( pressure = force per unit area ) • Pressure depends on • number of collisions per second • force acting per collision ( actually change Δ. m v in momentum ) F ...
... Kinetic Theory of Gases • Gas exerts a pressure because the particles hit wall of container ( pressure = force per unit area ) • Pressure depends on • number of collisions per second • force acting per collision ( actually change Δ. m v in momentum ) F ...
Simple Harmonic Motion
... Amplitude – The maximum displacement from equilibrium. Period – The time it takes to execute a complete cycle of motion. Frequency – The number of cycles or vibrations per unit of time. Period and frequency measure time. Frequency is the reciprocal of the period. ...
... Amplitude – The maximum displacement from equilibrium. Period – The time it takes to execute a complete cycle of motion. Frequency – The number of cycles or vibrations per unit of time. Period and frequency measure time. Frequency is the reciprocal of the period. ...
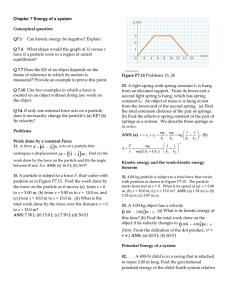
Chapter 7 Energy of a system Conceptual question Q7.1 Can kinetic
... where the particle can be found, (d) its maximum kinetic energy, (e) the location where it has maximum kinetic energy, and (f) the binding energy of the system—that is, the additional energy that it would have to be given in order for the particle to move out to r . ANS: (b) 5.6 J E 1 J ; (c) ...
... where the particle can be found, (d) its maximum kinetic energy, (e) the location where it has maximum kinetic energy, and (f) the binding energy of the system—that is, the additional energy that it would have to be given in order for the particle to move out to r . ANS: (b) 5.6 J E 1 J ; (c) ...
MT 5500 - Loyola College
... 5. If the distance x of a point moving on a straight line from a fixed origin on it and its velocity V are connected by , show that the motion is simple harmonic. 6. Find the length of a seconds pendulum. 7. If the angular velocity of a particle moving in a plane curve about a fixed origin is consta ...
... 5. If the distance x of a point moving on a straight line from a fixed origin on it and its velocity V are connected by , show that the motion is simple harmonic. 6. Find the length of a seconds pendulum. 7. If the angular velocity of a particle moving in a plane curve about a fixed origin is consta ...
M - Otterbein University
... Newton’s Laws of Motion (Axioms) 1. Every body continues in a state of rest or in a state of uniform motion in a straight line unless it is compelled to change that state by forces acting on it (law of inertia) ...
... Newton’s Laws of Motion (Axioms) 1. Every body continues in a state of rest or in a state of uniform motion in a straight line unless it is compelled to change that state by forces acting on it (law of inertia) ...
Lecture Notes for Section 13.4 (Equation of Motion)
... If the forces can be resolved directly from the free-body diagram (often the case in 2-D problems), use the scalar form of the equation of motion. In more complex cases (usually 3-D), a Cartesian vector is written for every force and a vector analysis is often best. A Cartesian vector formulation of ...
... If the forces can be resolved directly from the free-body diagram (often the case in 2-D problems), use the scalar form of the equation of motion. In more complex cases (usually 3-D), a Cartesian vector is written for every force and a vector analysis is often best. A Cartesian vector formulation of ...
Brownian motion

Brownian motion or pedesis (from Greek: πήδησις /pˈɪːdiːsis/ ""leaping"") is the random motion of particles suspended in a fluid (a liquid or a gas) resulting from their collision with the quick atoms or molecules in the gas or liquid. Wiener Process refers to the mathematical model used to describe such Brownian Motion, which is often called a particle theoryThis transport phenomenon is named after the botanist Robert Brown. In 1827, while looking through a microscope at particles trapped in cavities inside pollen grains in water, he noted that the particles moved through the water but was not able to determine the mechanisms that caused this motion. Atoms and molecules had long been theorized as the constituents of matter, and many decades later, Albert Einstein published a paper in 1905 that explained in precise detail how the motion that Brown had observed was a result of the pollen being moved by individual water molecules. This explanation of Brownian motion served as definitive confirmation that atoms and molecules actually exist, and was further verified experimentally by Jean Perrin in 1908. Perrin was awarded the Nobel Prize in Physics in 1926 ""for his work on the discontinuous structure of matter"" (Einstein had received the award five years earlier ""for his services to theoretical physics"" with specific citation of different research). The direction of the force of atomic bombardment is constantly changing, and at different times the particle is hit more on one side than another, leading to the seemingly random nature of the motion.The mathematical model of Brownian motion has numerous real-world applications. For instance, Stock market fluctuations are often cited, although Benoit Mandelbrot rejected its applicability to stock price movements in part because these are discontinuous.Brownian motion is among the simplest of the continuous-time stochastic (or probabilistic) processes, and it is a limit of both simpler and more complicated stochastic processes (see random walk and Donsker's theorem). This universality is closely related to the universality of the normal distribution. In both cases, it is often mathematical convenience, rather than the accuracy of the models, that motivates their use.