5.1 - Mass/Spring Systems
... After a mass is attached to a spring, it stretches the spring by an amount s to an ____________________ ____________ where it’s weight W is balanced by the restoring force F ks . Weight is defined by ____________ times ______________. _______________ can be measured in ...
... After a mass is attached to a spring, it stretches the spring by an amount s to an ____________________ ____________ where it’s weight W is balanced by the restoring force F ks . Weight is defined by ____________ times ______________. _______________ can be measured in ...
Shields` diagram - public.iastate.edu
... MEANING: The critical shear stress for incipient motion of cohesionless bed material normalized to the particles’ submerged unit weight. ...
... MEANING: The critical shear stress for incipient motion of cohesionless bed material normalized to the particles’ submerged unit weight. ...
RHIG - Wayne State University
... • Vanishing of dr/dt implies turning points • Two roots in general: rmin and rmax. • Motion confined to an annular region between rmin and rmax. • Certain combinations of E and l may lead to a single root: one then has a circular motion, and dr/dt = 0 at all times. ...
... • Vanishing of dr/dt implies turning points • Two roots in general: rmin and rmax. • Motion confined to an annular region between rmin and rmax. • Certain combinations of E and l may lead to a single root: one then has a circular motion, and dr/dt = 0 at all times. ...
1 - Ryoichi Kawai
... First Law: A body moves with constant velocity (which may be zero) unless acted on by a force. Second Law: The time rate of change of the momentum of a body equals the force acting on the body. Third Law: The forces two bodies apply to each other are equal in magnitude and opposite in direction. ...
... First Law: A body moves with constant velocity (which may be zero) unless acted on by a force. Second Law: The time rate of change of the momentum of a body equals the force acting on the body. Third Law: The forces two bodies apply to each other are equal in magnitude and opposite in direction. ...
Mechanics 105 chapter 12
... Causes displaced mass to to be restored to the equilibrium position. Potential energy Kinetic energy. At equilibrium – large KE but force is now zero. Newton’s first law - keeps moving. ...
... Causes displaced mass to to be restored to the equilibrium position. Potential energy Kinetic energy. At equilibrium – large KE but force is now zero. Newton’s first law - keeps moving. ...
January 2011 - Maths Genie
... Information for Candidates A booklet ‘Mathematical Formulae and Statistical Tables’ is provided. Full marks may be obtained for answers to ALL questions. There are 7 questions in this question paper. The total mark for this paper is 75. Advice to Candidates You must ensure that your answers to parts ...
... Information for Candidates A booklet ‘Mathematical Formulae and Statistical Tables’ is provided. Full marks may be obtained for answers to ALL questions. There are 7 questions in this question paper. The total mark for this paper is 75. Advice to Candidates You must ensure that your answers to parts ...
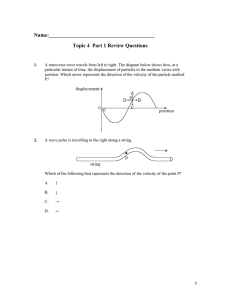
Topic 4 Part 1 Review Questions student 2015
... Which of the following graphs shows the variation with displacement x of the speed v of a particle performing simple harmonic motion. ...
... Which of the following graphs shows the variation with displacement x of the speed v of a particle performing simple harmonic motion. ...
Simple Harmonic Motion and Elastic Energy
... motion. The spring force is a restoring force always directed toward the equilibrium position. The Acceleration of an object in simple harmonic motion (SHM) is proportional to the displacement from equilibrium and oppositely directed. a=-(k/m)x is the result of applying Newton’s second law to a mass ...
... motion. The spring force is a restoring force always directed toward the equilibrium position. The Acceleration of an object in simple harmonic motion (SHM) is proportional to the displacement from equilibrium and oppositely directed. a=-(k/m)x is the result of applying Newton’s second law to a mass ...
ert146 lect kinetic of motion
... where FR is the resultant force, which is a vector summation of all the force produces the vector ma. To illustrate the equation, consider a particle acted on by two forces. First, draw the particle’s free-body diagram, showing all forces acting on the particle. Next, draw the kinetic diagram, showi ...
... where FR is the resultant force, which is a vector summation of all the force produces the vector ma. To illustrate the equation, consider a particle acted on by two forces. First, draw the particle’s free-body diagram, showing all forces acting on the particle. Next, draw the kinetic diagram, showi ...
Q1 Show that the solution of the two body problem is a - UR-CST
... 3. Answer to any 2 Questions in section B showing all working clearly. 4. Start every new question from a fresh page 5. Every question carries 15 marks in section B 6. Do not forget to write your Registration Number 7. Write all your answers in the booklet provided ...
... 3. Answer to any 2 Questions in section B showing all working clearly. 4. Start every new question from a fresh page 5. Every question carries 15 marks in section B 6. Do not forget to write your Registration Number 7. Write all your answers in the booklet provided ...
Brownian motion

Brownian motion or pedesis (from Greek: πήδησις /pˈɪːdiːsis/ ""leaping"") is the random motion of particles suspended in a fluid (a liquid or a gas) resulting from their collision with the quick atoms or molecules in the gas or liquid. Wiener Process refers to the mathematical model used to describe such Brownian Motion, which is often called a particle theoryThis transport phenomenon is named after the botanist Robert Brown. In 1827, while looking through a microscope at particles trapped in cavities inside pollen grains in water, he noted that the particles moved through the water but was not able to determine the mechanisms that caused this motion. Atoms and molecules had long been theorized as the constituents of matter, and many decades later, Albert Einstein published a paper in 1905 that explained in precise detail how the motion that Brown had observed was a result of the pollen being moved by individual water molecules. This explanation of Brownian motion served as definitive confirmation that atoms and molecules actually exist, and was further verified experimentally by Jean Perrin in 1908. Perrin was awarded the Nobel Prize in Physics in 1926 ""for his work on the discontinuous structure of matter"" (Einstein had received the award five years earlier ""for his services to theoretical physics"" with specific citation of different research). The direction of the force of atomic bombardment is constantly changing, and at different times the particle is hit more on one side than another, leading to the seemingly random nature of the motion.The mathematical model of Brownian motion has numerous real-world applications. For instance, Stock market fluctuations are often cited, although Benoit Mandelbrot rejected its applicability to stock price movements in part because these are discontinuous.Brownian motion is among the simplest of the continuous-time stochastic (or probabilistic) processes, and it is a limit of both simpler and more complicated stochastic processes (see random walk and Donsker's theorem). This universality is closely related to the universality of the normal distribution. In both cases, it is often mathematical convenience, rather than the accuracy of the models, that motivates their use.