Algebra Curriculum Guide – Unit 1 Expressions
... UNDERSTANDINGS Students will understand that… Every number has a decimal expansion. The value of any real number can be represented in relation to other real numbers such as with decimals converted to fractions, scientific notation and numbers written with exponents (8 = 23 ). Properties of op ...
... UNDERSTANDINGS Students will understand that… Every number has a decimal expansion. The value of any real number can be represented in relation to other real numbers such as with decimals converted to fractions, scientific notation and numbers written with exponents (8 = 23 ). Properties of op ...
1 Chapter III Set Theory as a Theory of First Order Predicate Logic
... Cohen's result, involving new axioms which settle the CH one way or thev other, none of the new axioms that were proposed seem to qualify as unequivocally true. So, from a conceptual point of view the CH is na open question to this day For our present purposes the first question - What is the total ...
... Cohen's result, involving new axioms which settle the CH one way or thev other, none of the new axioms that were proposed seem to qualify as unequivocally true. So, from a conceptual point of view the CH is na open question to this day For our present purposes the first question - What is the total ...
Automata vs. Logics on Data Words
... into equivalent automaton-based specifications, easing, in this way, the various reasoning tasks. Different models of automata which process words over infinite alphabets have been proposed and studied in the literature (see, for instance, the surveys [6, 7]). Pebble automata [8] use special markers ...
... into equivalent automaton-based specifications, easing, in this way, the various reasoning tasks. Different models of automata which process words over infinite alphabets have been proposed and studied in the literature (see, for instance, the surveys [6, 7]). Pebble automata [8] use special markers ...
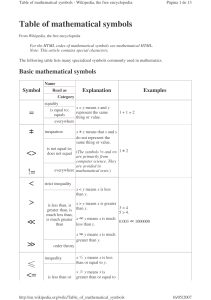
Table of mathematical symbols
... random variable X has has distribution the probability statistics distribution D. ...
... random variable X has has distribution the probability statistics distribution D. ...
Holt McDougal Algebra 1 6-2
... , where t is the number of days since start of the experiment. Find the population of the colony on the 8th day. ...
... , where t is the number of days since start of the experiment. Find the population of the colony on the 8th day. ...
Rational Exponents
... , where t is the number of days since start of the experiment. Find the population of the colony on the 8th day. ...
... , where t is the number of days since start of the experiment. Find the population of the colony on the 8th day. ...
MoL-2013-07 - Institute for Logic, Language and Computation
... In this thesis, we are (for the most part) not interested in this interplay between a modeltransformation technique and sentences in the language of set theory, but instead, in the purely modal side of these techniques. That is, we are interested in understanding the general principles that are true ...
... In this thesis, we are (for the most part) not interested in this interplay between a modeltransformation technique and sentences in the language of set theory, but instead, in the purely modal side of these techniques. That is, we are interested in understanding the general principles that are true ...
When Bi-Interpretability Implies Synonymy
... We are interested in theories with coding. There are several ‘degrees’ of coding, like pairing, sequences, etcetera. We want a notion that allows us to build arbitrary sequences of all objects of our domain. The relevant notion is sequentiality. We also define a wider notion conceptuality. This last ...
... We are interested in theories with coding. There are several ‘degrees’ of coding, like pairing, sequences, etcetera. We want a notion that allows us to build arbitrary sequences of all objects of our domain. The relevant notion is sequentiality. We also define a wider notion conceptuality. This last ...
210ch2 - Dr. Djamel Bouchaffra
... Note: f associates with each x in A one and only one y in B. A is called the domain and B is called the codomain. If f(x) = y y is called the image of x under f x is called a preimage of y (note there may be more than one preimage of y but there is only one image of x). The range of f is the set of ...
... Note: f associates with each x in A one and only one y in B. A is called the domain and B is called the codomain. If f(x) = y y is called the image of x under f x is called a preimage of y (note there may be more than one preimage of y but there is only one image of x). The range of f is the set of ...
A Logical Expression of Reasoning
... thus simply defined as those inferences which are not deductive. For the sake of clarity and more specificity, here we call those inferences which are not deductive as forming the class of ampliative inferences, and reserve the term induction to a special subclass of it. In what this subclass consis ...
... thus simply defined as those inferences which are not deductive. For the sake of clarity and more specificity, here we call those inferences which are not deductive as forming the class of ampliative inferences, and reserve the term induction to a special subclass of it. In what this subclass consis ...
Methods of Proof Ch 11
... colour any map so that no countries with a common border had the same colour. This conjecture was finally proven in 1976, having first been put forward in 1852. Fermat’s Last Theorem: This stated for n, an integer greater than two, there are no positive integer values x, y, and z such that xn + yn = ...
... colour any map so that no countries with a common border had the same colour. This conjecture was finally proven in 1976, having first been put forward in 1852. Fermat’s Last Theorem: This stated for n, an integer greater than two, there are no positive integer values x, y, and z such that xn + yn = ...