A General Procedure for Hypothesis Testing
... • If we say that Prof. Bee has a score of 1.5 on his student evaluations and Prof. Cee has a score of 2.3 on his student evaluations, can we then say Prof. Bee is better than Prof. Cee? The answer is NO. This difference could have resulted by chance. Remember that we look at the amount of variation ...
... • If we say that Prof. Bee has a score of 1.5 on his student evaluations and Prof. Cee has a score of 2.3 on his student evaluations, can we then say Prof. Bee is better than Prof. Cee? The answer is NO. This difference could have resulted by chance. Remember that we look at the amount of variation ...
Procedure - Web4students
... Part 1: Construct a 98% confidence interval estimate for the mean pH levels of rain in that area for the year 2000. Part 2: At the 1% significance level, test the claim of the biologist that the pH level of the rain in that area has decreased, and therefore, the acidity of the rain has increased. Pr ...
... Part 1: Construct a 98% confidence interval estimate for the mean pH levels of rain in that area for the year 2000. Part 2: At the 1% significance level, test the claim of the biologist that the pH level of the rain in that area has decreased, and therefore, the acidity of the rain has increased. Pr ...
Estimating the Value of a Parameter Using Confidence Intervals
... The news release isn't saying that the average of time spent for all employed persons is 7.6 hours per day they're referring to those in the sample of 12,250 individuals in the study. Both of these examples are called point estimates. 50%, for example, is the point estimate for the percentage of all ...
... The news release isn't saying that the average of time spent for all employed persons is 7.6 hours per day they're referring to those in the sample of 12,250 individuals in the study. Both of these examples are called point estimates. 50%, for example, is the point estimate for the percentage of all ...
Chap008 - Ka
... Here is unknown, so we estimate it with the sample standard deviation s. As long as the sample size n 30, z can be approximated with: ...
... Here is unknown, so we estimate it with the sample standard deviation s. As long as the sample size n 30, z can be approximated with: ...
6.6 The Central Limit Theorem 6.6.1 State the Central Limit Theorem
... If we are applying a one-tailed test, there is only one critical value. If we are applying a two-tailed test, there are two critical values. The following diagram illustrates the critical values for a two-tailed test, at the 0.01 level of significance. Since this is a two-tailed test, half of the 0. ...
... If we are applying a one-tailed test, there is only one critical value. If we are applying a two-tailed test, there are two critical values. The following diagram illustrates the critical values for a two-tailed test, at the 0.01 level of significance. Since this is a two-tailed test, half of the 0. ...
Regression - UMass Math
... (Note that the F test assumes the burn times are independent and normal with the same variance.) ...
... (Note that the F test assumes the burn times are independent and normal with the same variance.) ...
SECTION 1
... b.) The shape is rather symmetric if you ignore the 2 smallest. The center of the distribution is about 13.9%. The spread is 1 or 2% from center. ...
... b.) The shape is rather symmetric if you ignore the 2 smallest. The center of the distribution is about 13.9%. The spread is 1 or 2% from center. ...
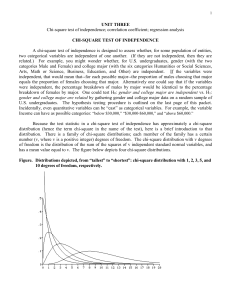
unit three - KSU Web Home
... 3. VAR() = 2 (VAR(Y) = 2). This may be called the equal variances assumption. (Another name for equal variances is homoskedasticity. A name for unequal variances is heteroskedasticity.) For any two entities: 4. the respective ’s are independent ( the respective Y’s are independent). This may b ...
... 3. VAR() = 2 (VAR(Y) = 2). This may be called the equal variances assumption. (Another name for equal variances is homoskedasticity. A name for unequal variances is heteroskedasticity.) For any two entities: 4. the respective ’s are independent ( the respective Y’s are independent). This may b ...
Normal Distribution
... It is good to know the standard deviation, because we can say that any value is: likely to be within 1 standard deviation (68 out of 100 should be) very likely to be within 2 standard deviations (95 out of 100 should be) almost certainly within 3 standard deviations (997 out of 1000 should be) ...
... It is good to know the standard deviation, because we can say that any value is: likely to be within 1 standard deviation (68 out of 100 should be) very likely to be within 2 standard deviations (95 out of 100 should be) almost certainly within 3 standard deviations (997 out of 1000 should be) ...
Bootstrapping (statistics)

In statistics, bootstrapping can refer to any test or metric that relies on random sampling with replacement. Bootstrapping allows assigning measures of accuracy (defined in terms of bias, variance, confidence intervals, prediction error or some other such measure) to sample estimates. This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods. Generally, it falls in the broader class of resampling methods.Bootstrapping is the practice of estimating properties of an estimator (such as its variance) by measuring those properties when sampling from an approximating distribution. One standard choice for an approximating distribution is the empirical distribution function of the observed data. In the case where a set of observations can be assumed to be from an independent and identically distributed population, this can be implemented by constructing a number of resamples with replacement, of the observed dataset (and of equal size to the observed dataset).It may also be used for constructing hypothesis tests. It is often used as an alternative to statistical inference based on the assumption of a parametric model when that assumption is in doubt, or where parametric inference is impossible or requires complicated formulas for the calculation of standard errors.