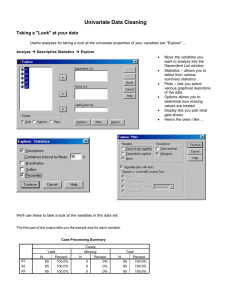
Lecture 8 - The Department of Mathematics & Statistics
... 1. A die is rolled and X = number of spots showing on the upper face. 2. Two dice are rolled and X = Total number of spots showing on the two upper faces. 3. A coin is tossed n = 100 times and X = number of times the coin toss resulted in a head. 4. A person is selected at random from a population a ...
... 1. A die is rolled and X = number of spots showing on the upper face. 2. Two dice are rolled and X = Total number of spots showing on the two upper faces. 3. A coin is tossed n = 100 times and X = number of times the coin toss resulted in a head. 4. A person is selected at random from a population a ...
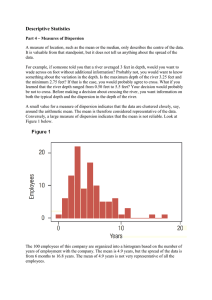
6 Descriptive Statistics
... the population size. Why isn’t the sample variance calculated with n, the sample size? • The true variance is based on data deviations from the true mean, μ. • The sample calculation is based on the data deviations from x-bar, not μ. X-bar is an estimator of μ; close but not the same. So the n-1 div ...
... the population size. Why isn’t the sample variance calculated with n, the sample size? • The true variance is based on data deviations from the true mean, μ. • The sample calculation is based on the data deviations from x-bar, not μ. X-bar is an estimator of μ; close but not the same. So the n-1 div ...
+ Confidence Intervals: The Basics
... results for our estimate. Statistical inference uses the language of probability to express the strength of our conclusions by taking chance variation due to random selection or random assignment into account. In this chapter, we’ll learn one method of statistical inference – confidence intervals – ...
... results for our estimate. Statistical inference uses the language of probability to express the strength of our conclusions by taking chance variation due to random selection or random assignment into account. In this chapter, we’ll learn one method of statistical inference – confidence intervals – ...
Chapter 6: The Normal Distribution
... We will continue with the model for IQ score of 12-year-olds. In answering the following questions, remember to use the symmetry of the normal distribution and the fact that the total area under the curve is 1. It may also be very useful to draw a picture of the area you are trying to find so you ca ...
... We will continue with the model for IQ score of 12-year-olds. In answering the following questions, remember to use the symmetry of the normal distribution and the fact that the total area under the curve is 1. It may also be very useful to draw a picture of the area you are trying to find so you ca ...
Research and Data Analysis
... within 1 to 2 standard deviations from the population mean • By the same token, for 95% of samples, the population mean will be within + or - 2 standard error units from the sample mean • E.g., for C.I. 80%, first find the lower and upper t-values that bind 80% area of the distribution. • Can state: ...
... within 1 to 2 standard deviations from the population mean • By the same token, for 95% of samples, the population mean will be within + or - 2 standard error units from the sample mean • E.g., for C.I. 80%, first find the lower and upper t-values that bind 80% area of the distribution. • Can state: ...
INSTITUTE OF BANKERS IN MALAWI DIPLOMA IN BANKING
... rural village, a random sample of 400 villagers was taken. The sample mean was found to be K35.00 with a sample standard deviation of K25.00. ...
... rural village, a random sample of 400 villagers was taken. The sample mean was found to be K35.00 with a sample standard deviation of K25.00. ...
Poll: Iraq speeches, election don`t help Bush
... sample proportion p̂ is approximately normal with mean p and standard deviation p 1 p ...
... sample proportion p̂ is approximately normal with mean p and standard deviation p 1 p ...
Mean deviation
... usually denoted by Var(X) or 2 . If you now look at the definition above, there are 3 parts to it. So for a raw data of a set of n observations: (i) Deviations from mean of the observations (xi x) ...
... usually denoted by Var(X) or 2 . If you now look at the definition above, there are 3 parts to it. So for a raw data of a set of n observations: (i) Deviations from mean of the observations (xi x) ...
joaquin_dana_ca08
... The sum of each PDF for each sample size n was computed using MATLAB’s sum function. In addition, the mean, variance and standard deviation for each n was computed as well. A histogram plot of the sums of random variables was plotted using MATLAB’s histogram function. Next, each sample size sum’s me ...
... The sum of each PDF for each sample size n was computed using MATLAB’s sum function. In addition, the mean, variance and standard deviation for each n was computed as well. A histogram plot of the sums of random variables was plotted using MATLAB’s histogram function. Next, each sample size sum’s me ...
confidence interval
... A researcher wishes to estimate the number of days it takes an automobile dealer to sell a Chevrolet Aveo. A sample of 50 cars had a mean time on the dealer’s lot of 54 days. Assume the population standard deviation to be 6.0 days. Find the best point estimate of the population mean and the 95% conf ...
... A researcher wishes to estimate the number of days it takes an automobile dealer to sell a Chevrolet Aveo. A sample of 50 cars had a mean time on the dealer’s lot of 54 days. Assume the population standard deviation to be 6.0 days. Find the best point estimate of the population mean and the 95% conf ...
Simple Linear Regression
... relationship between a dependent variable (usually called y) and an independent variable (usually called x). The dependent variable is the variable for which we want to make a prediction. While various non-linear forms may be used, simple linear regression models are the most common. ...
... relationship between a dependent variable (usually called y) and an independent variable (usually called x). The dependent variable is the variable for which we want to make a prediction. While various non-linear forms may be used, simple linear regression models are the most common. ...
Bootstrapping (statistics)

In statistics, bootstrapping can refer to any test or metric that relies on random sampling with replacement. Bootstrapping allows assigning measures of accuracy (defined in terms of bias, variance, confidence intervals, prediction error or some other such measure) to sample estimates. This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods. Generally, it falls in the broader class of resampling methods.Bootstrapping is the practice of estimating properties of an estimator (such as its variance) by measuring those properties when sampling from an approximating distribution. One standard choice for an approximating distribution is the empirical distribution function of the observed data. In the case where a set of observations can be assumed to be from an independent and identically distributed population, this can be implemented by constructing a number of resamples with replacement, of the observed dataset (and of equal size to the observed dataset).It may also be used for constructing hypothesis tests. It is often used as an alternative to statistical inference based on the assumption of a parametric model when that assumption is in doubt, or where parametric inference is impossible or requires complicated formulas for the calculation of standard errors.