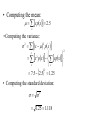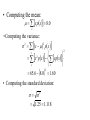Download Lecture 8 - The Department of Mathematics & Statistics

The two way frequency table
The c2 statistic
Techniques for examining
dependence amongst two categorical
variables
Situation
•
•
•
•
We have two categorical variables R and C.
The number of categories of R is r.
The number of categories of C is c.
We observe n subjects from the population and
count
xij = the number of subjects for which R = i and
C = j.
• R = rows, C = columns
Example
Both Systolic Blood pressure (C) and Serum
Chlosterol (R) were meansured for a sample of n
= 1237 subjects.
The categories for Blood Pressure are:
<126 127-146 147-166
167+
The categories for Chlosterol are:
<200 200-219 220-259
260+
Table: two-way frequency
Systolic Blood pressure
Serum
Cholesterol
<127
127-146
147-166
167+
Total
< 200
117
121
47
22
307
200-219
85
98
43
20
246
220-259
115
209
68
43
439
260+
67
99
46
33
245
Total
388
527
204
118
1237
3 dimensional bargraph
Example
This comes from the drug use data.
The two variables are:
1. Age (C) and
2. Antidepressant Use (R)
measured for a sample of n = 33,957 subjects.
Two-way Frequency Table
Took anti-depressants - 12 mo * Age - (G) Crosstabulation
Count
Took anti-depres s ants
- 12 mo
Total
YES
NO
20-29
322
5007
5329
30-39
523
6201
6724
Age - (G)
40-49
50-59
570
522
5822
4982
6392
5504
60-69
265
4114
4379
70+
249
5380
5629
Total
2451
31506
33957
Percentage antidepressant use vs Age
20-29
6.04%
Age - (G)
30-39
40-49
50-59
7.78%
8.92%
9.48%
60-69
6.05%
70+
4.42%
Antidepressant Use vs Age
10.0%
5.0%
0.0%
20-29
30-39
40-49
50-59
60-69
70+
The c2 statistic for measuring dependence
amongst two categorical variables
Define
c
Ri   xij  i th row Total
j 1
c
C j   xij  j
th
column Total
i 1
Eij 
Ri C j
n
= Expected frequency in the (i,j) th cell in
the case of independence.
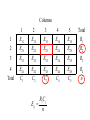
Columns
1
2
3
4
5
Total
1
2
x11
x21
x12
x22
x13
x23
x14
x24
x15
x25
R1
R2
3
x31
x32
x33
x34
x35
R3
4
Total
x41
C1
x42
C2
x43
C3
x44
C4
x45
C5
R4
N
c
Ri   xij  i th row Total
j 1
c
C j   xij  j th column Total
i 1
Columns
1
2
3
4
5
Total
1
2
E11
E21
E12
E22
E13
E23
E14
E24
E15
E25
R1
R2
3
E31
E32
E33
E34
E35
R3
4
Total
E41
C1
E42
C2
E43
C3
E44
C4
E45
C5
R4
n
Eij 
Ri C j
n
if Eij 
Justification
Ri C j
Eij
then
n
Ri

Cj
n
Proportion in column j for row i
overall proportion in column j
1
2
3
4
5
Total
1
E11
E12
E13
E14
E15
R1
2
E21
E22
E23
E24
E25
R2
3
E31
E32
E33
E34
E35
R3
4
E41
E42
E43
E44
E45
R4
Total
C1
C2
C3
C4
C5
n
if Eij 
and
Ri C j
Eij
Ri

Cj
n
then
n
Proportion in row i for column j
overall proportion in row i
1
2
3
4
5
Total
1
E11
E12
E13
E14
E15
R1
2
E21
E22
E23
E24
E25
R2
3
E31
E32
E33
E34
E35
R3
4
E41
E42
E43
E44
E45
R4
Total
C1
C2
C3
C4
C5
n
The c2 statistic
r
c
c  
2
i 1 j 1
x
ij
 Eij 
2
Eij
Eij= Expected frequency in the (i,j) th cell
in the case of independence.
xij= observed frequency in the (i,j) th cell
Example: studying the relationship between
Systolic Blood pressure and Serum Cholesterol
In this example we are interested in whether
Systolic Blood pressure and Serum Cholesterol
are related or whether they are independent.
Both were measured for a sample of n = 1237
cases
Observed frequencies
Systolic Blood pressure
Serum
Cholesterol
<127
127-146
147-166
167+
Total
< 200
117
121
47
22
307
200-219
85
98
43
20
246
220-259
115
209
68
43
439
260+
67
99
46
33
245
Total
388
527
204
118
1237
Expected frequencies
Systolic Blood pressure
Serum
Cholesterol
<127
127-146
147-166
167+
Total
< 200
96.29
130.79
50.63
29.29
307
200-219
77.16
104.8
40.47
23.47
246
220-259
137.70
187.03
72.40
41.88
439
260+
76.85
104.38
40.04
23.37
245
Total
388
527
204
118
1237
In the case of independence the distribution across a row is the
same for each row
The distribution down a column is the same for each column
Table
Expected frequencies, Observed frequencies, Standardized Residuals
Serum
Cholesterol
<200
200-219
220-259
260+
Total
c2
= 20.85
<127
96.29
(117)
2.11
77.16
(85)
0.86
137.70
(119)
-1.59
76.85
(67)
-1.12
388
Systolic Blood pressure
127-146
147-166
130.79
50.63
(121)
(47)
-0.86
-0.51
104.80
40.47
(98)
(43)
-0.66
0.38
187.03
72.40
(209)
(68)
1.61
-0.52
104.38
40.04
(99)
(46)
-0.53
0.88
527
204
rij

x

ij
 Eij 
Eij
167+
29.29
(22)
-1.35
23.47
(20)
-0.72
41.88
(43)
0.17
23.37
(33)
1.99
118
Total
307
246
439
245
1237
Standardized residuals
rij

x

ij
 Eij 
Eij
The c2 statistic
r
c
c 2  
i 1 j 1
x
ij  Eij 
2
Eij
r
c
 rij2  20.85
i 1 j 1
Properties of the c2 statistic
1. The c2 statistic is always positive.
2. Small values of c2 indicate that Rows and
Columns are independent. In this case will
be in the range of (r – 1)(c – 1).
3. Large values of c2 indicate that Rows and
columns are not independent.
4. Later on we will discuss this in more detail
(when we study Hypothesis Testing).
Example
This comes from the drug use data.
The two variables are:
1. Role (C) and
2. Antidepressant Use (R)
measured for a sample of n = 33,957 subjects.
Two-way Frequency Table
Took anti-depressants - 12 mo * role Crosstabulation
Count
role
Took anti-depres sants
- 12 mo
YES
NO
Total
parent,
partner,
worker
344
6268
6612
parent,
partner
101
967
1068
parent, worker
201
1150
1351
partner,
worker
275
5150
5425
worker only
455
5249
5704
parent only
63
392
455
partner only
224
3036
3260
no roles
414
2679
3093
Total
2077
24891
26968
Percentage antidepressant use vs Role
Role
parent,
partner,
worker
parent,
partner
parent,
worker
partner,
worker
worker
only
5.20%
9.46%
14.88%
5.07%
7.98%
parent only
partner
only
no roles
13.85%
6.87%
13.39%
Antidepressant Use vs Role
c2 = 381.961
20.0%
15.0%
10.0%
5.0%
0.0%
parent,
partner,
worker
parent,
partner
parent,
worker
partner,
worker
worker
only
parent
only
partner no roles
only
Calculation of c2
The Raw data
YES
NO
Total
1
344
6268
6612
2
101
967
1068
3
201
1150
1351
4
275
5150
5425
5
455
5249
5704
6
63
392
455
7
224
3036
3260
4
417.82
5007.18
5425
5
439.31
5264.69
5704
6
35.04
419.96
455
7
251.08
3008.92
3260
8
414
2679
3093
Total
2077
24891
26968
Expected frequencies
YES
NO
Total (C j )
1
509.24
6102.76
6612
2
82.25
985.75
1068
Eij 
3
104.05
1246.95
1351
Ri C j
n
rij

x

ij
 Eij 
Eij
Total (R i )
8
238.21
2077
2854.79
24891
3093
26968
The Residuals
1
-7.32
2.12
YES
NO
2
2.07
-0.60
3
9.50
-2.75
rij

x

ij
4
-6.99
2.02
5
0.75
-0.22
6
4.72
-1.36
 Eij 
Eij
The calculation of c2
c   r  
2
2
ij
i
j
i
j
x
ij
 Eij 
Eij
2
 381.961
7
-1.71
0.49
8
11.39
-3.29
Probability Theory
Modelling random phenomena
Some counting formulae
Permutations
the number of ways that you can order n
objects is:
n! = n(n-1)(n-2)(n-3)…(3)(2)(1)
Example:
the number of ways you can order the three
letters A, B, and C is 3! = 3(2)(1) = 6
ABC ACB BAC BCA CAB CBA
Definition
0! = 1
Reason
mathematical consistency.
In many of the formulae given later, this
definition leads to consistency.
Permutations
the number of ways that you can choose k
objects from n objects in a specific order:
n!
 n(n  1) (n  k  1)
n Pk 
(n  k )!
Example:
the number of ways you choose two letters
from the four letters A, B, D, C in a specific
order is
4!
4!
  (4)(3)  12
4 P2 
(4  2)! 2!
AB BA AC
BC CB BD
CA AD DA
DB CD DC
Example:
Suppose that we have a committee of 10
people. We want to choose a chairman, a
vice-chairman, and a treasurer for the
committee. The chairman is chosen first, the
vice chairman second and the treasures
third. How many ways can this be done.
n!
 n(n  1) (n  k  1)
n Pk 
(n  k )!
10!
10!

 (10)(9)(8)  720
10 P3 
(10  3)! 7!
Example:
How many ways can we order n objects.
Answer
n!
or
Choose n objects from n objects in a
specific order
n!
n!
  n ! if 0!  1.
n Pn 
(n  n)! 0!
This is what is meant by the statement that the
definition 0! = 1 leads to mathematical consistency
Combinations
the number of ways that you can choose k
objects from n objects (order irrelevant) is:
n
n!
n(n  1) (n  k  1)
n Ck  
 k   k!(n  k )! 
k (k  1) (1)
 
Example:
the number of ways you choose two letters
from the four letters A, B, D, C
 4
4!
4! (4)(3) 12






6
4 C2  
 2  2!(4  2)! 2!2! (2)(1) 2
 
{A,B} {A,C} {A,D} {B,C} {B,D}{C,D}
Example:
Suppose we have a committee of 10 people
and we want to choose a sub-committee of
3 people. How many ways can this be done
10  10! (10)(9)(3)
10 C3  
 3   3!7!  (3)( 2)(1)  45
 
Example: Random sampling
Suppose we have a club of N =1000 persons and
we want to choose sample of k = 250 of these
individuals to determine there opinion on a given
issue. How many ways can this be performed?
1000 
1000!
242



4
.
823

10
1000 C250  
 250  250!750!


The choice of the sample is called random
sampling if all of the choices has the same
probability of being selected
Important Note:
0! is always defined to be 1.
Also
n
n!
n
Ck    
 k  k!(n  k )!
are called Binomial Coefficients
Reason:
The Binomial Theorem
x  y 
n
C0 x y  n C1 x y
0
n

n
1
n 1
 n C2 x y
2
n2
   n Cn x y
n
0
 n  0 n  n  1 n1  n  2 n 2
 n n 0
   x y    x y    x y    x y
0
1
 2
 n
Binomial Coefficients can also be
calculated using Pascal’s triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
Random Variables
Probability distributions
Definition:
A random variable X is a number whose
value is determined by the outcome of a
random experiment (random phenomena)
Examples
1. A die is rolled and X = number of spots
showing on the upper face.
2. Two dice are rolled and X = Total number
of spots showing on the two upper faces.
3. A coin is tossed n = 100 times and
X = number of times the coin toss
resulted in a head.
4. A person is selected at random from a
population and
X = weight of that individual.
5. A sample of n = 100 individuals are
selected at random from a population (i.e.
all samples of n = 100 have the same
probability of being selected) .
X = the average weight of the 100
individuals.
In all of these examples X fits the definition
of a random variable, namely:
– a number whose value is determined by the
outcome of a random experiment (random
phenomena)
Random variables are either
• Discrete
– Integer valued
– The set of possible values for X are integers
• Continuous
– The set of possible values for X are all real
numbers
– Range over a continuum.
Examples
• Discrete
– A die is rolled and X = number of spots
showing on the upper face.
– Two dice are rolled and X = Total
number of spots showing on the two
upper faces.
– A coin is tossed n = 100 times and X =
number of times the coin toss resulted
in a head.
Examples
• Continuous
–
–
A person is selected at random from a
population and X = weight of that individual.
A sample of n = 100 individuals are selected
at random from a population (i.e. all samples
of n = 100 have the same probability of being
selected) . X = the average weight of the 100
individuals.
Probability distribution of a
Random Variable
The probability distribution of a
discrete random variable is describe
by its :
probability function p(x).
p(x) = the probability that X takes on
the value x.
Examples
• Discrete
– A die is rolled and X = number of spots
showing on the upper face.
x
1
p(x) 1/6
2
1/6
3
1/6
4
1/6
5
1/6
6
1/6
– Two dice are rolled and X = Total
number of spots showing on the two
upper faces.
x
2
3
4
5
6
7
8
9
10
11
12
p(x) 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36
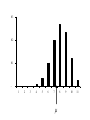
Graphs
To plot a graph of p(x), draw bars of height
p(x) above each value of x.
Rolling a die
0
1
2
3
4
5
6
Rolling two dice
0
Note:
1. 0  p(x)  1
2.
 p x   1
x
b
3.
Pa  X  b   p( x)
x a
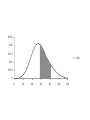
The probability distribution of a
continuous random variable is
described by its :
probability density curve f(x).
i.e. a curve which has the following
properties :
• 1. f(x) is always positive.
• 2. The total are under the curve f(x) is one.
• 3. The area under the curve f(x) between a
and b is the probability that X lies between the
two values.
0.025
0.02
0.015
f(x)
0.01
0.005
0
0
20
40
60
80
100
120
An Important discrete distribution
The Binomial distribution
Suppose we have an experiment with two
outcomes – Success(S) and Failure(F).
Let p denote the probability of S (Success).
In this case q=1-p denotes the probability of
Failure(F).
Now suppose this experiment is repeated n
times independently.
Let X denote the number of successes
occuring in the n repititions.
Then X is a random variable.
It’s possible values are
0, 1, 2, 3, 4, … , (n – 2), (n – 1), n
and p(x) for any of the above values of x is
given by:
 n x
 n  x n x
n x
px     p 1  p     p q
 x
 x
X is said to have the Binomial
distribution with parameters n and p.
Summary:
X is said to have the Binomial distribution
with parameters n and p.
1. X is the number of successes occuring in
the n repititions of a Success-Failure
Experiment.
2. The probability of success is p.
3.
n
px     p 1  p 
 x
x
n x
Examples:
1. A coin is tossed n = 5 times. X is the
number of heads occuring in the 5 tosses
of the coin. In this case p = ½ and
 5  1 x 1 5 x  5  1 5  5  1
px     2   2     2     32 
 x
 x
 x
x
0
1
2
3
4
5
p(x)
1
32
5
32
10
32
10
32
5
32
1
32
Random Variables
Numerical Quantities whose values
are determine by the outcome of a
random experiment
Discrete Random Variables
Discrete Random Variable: A random variable
usually assuming an integer value.
• a discrete random variable assumes values that are
isolated points along the real line. That is neighbouring
values are not “possible values” for a discrete random
variable
Note: Usually associated with counting
• The number of times a head occurs in 10 tosses of a coin
• The number of auto accidents occurring on a weekend
• The size of a family
Continuous Random Variables
Continuous Random Variable: A quantitative random
variable that can vary over a continuum
• A continuous random variable can assume any value
along a line interval, including every possible value
between any two points on the line
Note: Usually associated with a measurement
• Blood Pressure
• Weight gain
• Height
Probability Distributions
of a Discrete Random Variable
Probability Distribution & Function
Probability Distribution: A mathematical
description of how probabilities are distributed with
each of the possible values of a random variable.
Notes:

The probability distribution allows one to determine probabilities
of events related to the values of a random variable.

The probability distribution may be presented in the form of a
table, chart, formula.
Probability Function: A rule that assigns probabilities to
the values of the random variable
Example
In baseball the number of individuals, X, on base when a
home run is hit ranges in value from 0 to 3. The
probability distribution is known and is given below:
x
p(x)
0
6/14
1
4/14
2
3/14
3
1/14
Note:
 This chart implies the only values x takes on are 0, 1, 2, and 3.
 If the random variable X is observed repeatedly the probabilities,
p(x), represents the proportion times the value x appears in that
sequence.
3


P( the random variable X equals 2) p (2)
14
3 1
4
Pthe random variable X is at least 2  p2  p3   
14 14 14
A Bar Graph
0.500
0.429
No. of persons on base
when a home run is hit
0.400
0.286
p(x)
0.300
0.214
0.200
0.100
0.071
0.000
0
1
2
# on base
3
Comments:
Every probability function must satisfy:
1. The probability assigned to each value of the
random variable must be between 0 and 1,
inclusive:
0  p( x)  1
2. The sum of the probabilities assigned to all the
values of the random variable must equal 1:
 p( x)  1
x
b
3. Pa  X  b   p( x)
x a
 p(a)  p(a  1)    p(b)
Mean and Variance of a
Discrete Probability Distribution
• Describe the center and spread of a
probability distribution
• The mean (denoted by greek letter m (mu)),
measures the centre of the distribution.
• The variance (s2) and the standard deviation (s)
measure the spread of the distribution.
s is the greek letter for s.
Mean of a Discrete Random Variable
• The mean, m, of a discrete random variable x is found by
multiplying each possible value of x by its own
probability and then adding all the products together:
m   xpx 
x
 x1 px1   x2 px2     xk pxk 
Notes:

The mean is a weighted average of the values of X.

The mean is the long-run average value of the random
variable.

The mean is centre of gravity of the probability
distribution of the random variable
0.3
0.2
0.1
1
2
3
4
5
6
7
8
m
9
10
11
Variance and Standard Deviation
Variance of a Discrete Random Variable: Variance, s2, of a
discrete random variable x is found by multiplying each possible
value of the squared deviation from the mean, (x  m)2, by its own
probability and then adding all the products together:


s 2   x  m 2 px 
2
x


2
  x px   xpx 
x
x

  x 2 px  m 2
x
Standard Deviation of a Discrete Random Variable: The positive
square root of the variance:
s  s2
Example
The number of individuals, X, on base when a home run
is hit ranges in value from 0 to 3.
x
0
1
2
3
Total
p (x )
xp(x)
0.429
0.000
0.286
0.286
0.214
0.429
0.071
0.214
1.000
0.929
 p(x)  xp(x)
x
2
0
1
4
9
2
x p(x)
0.000
0.286
0.857
0.643
1.786
2
x
 p( x)
• Computing the mean:
m   xpx   0.929
x
Note:
• 0.929 is the long-run average value of the random
variable
• 0.929 is the centre of gravity value of the probability
distribution of the random variable
• Computing the variance:


s 2   x  m 2 px 
2
x


2
  x px   xpx 
x
x

 1.786  .929  0.923
2
• Computing the standard deviation:
s  s2
 0.923  0.961
The Binomial distribution
1. We have an experiment with two outcomes
– Success(S) and Failure(F).
2. Let p denote the probability of S (Success).
3. In this case q=1-p denotes the probability of
Failure(F).
4. This experiment is repeated n times
independently.
5. X denote the number of successes occuring in the
n repititions.
The possible values of X are
0, 1, 2, 3, 4, … , (n – 2), (n – 1), n
and p(x) for any of the above values of x is
given by:
 n x
 n  x n x
n x
px     p 1  p     p q
 x
 x
X is said to have the Binomial distribution
with parameters n and p.
Summary:
X is said to have the Binomial distribution with
parameters n and p.
1. X is the number of successes occurring in the n
repetitions of a Success-Failure Experiment.
2. The probability of success is p.
3. The probability function
n x
n x
px     p 1  p 
 x
Example:
1. A coin is tossed n = 5 times. X is the
number of heads occurring in the 5 tosses
of the coin. In this case p = ½ and
 5  1 x 1 5 x  5  1 5  5  1
px     2   2     2     32 
 x
 x
 x
x
0
1
2
3
4
5
p(x)
1
32
5
32
10
32
10
32
5
32
1
32
0.4
p (x )
0.3
0.2
0.1
0.0
1
2
3
4
number of heads
5
6
Computing the summary parameters for the
distribution – m, s2, s
x
0
1
2
3
4
5
Total
p (x )
0.03125
0.15625
0.31250
0.31250
0.15625
0.03125
1.000
 p(x)
xp(x)
0.000
0.156
0.625
0.938
0.625
0.156
2.500
 xp(x)
x
2
0
1
4
9
16
25
2
x p(x)
0.000
0.156
1.250
2.813
2.500
0.781
7.500
2
x
 p( x)
• Computing the mean:
m   xpx   2.5
x
• Computing the variance:


s 2   x  m 2 px 
2
x


2
  x px   xpx 
x
x

 7.5  2.5  1.25
2
• Computing the standard deviation:
s  s2
 1.25  1.118
Example:
• A surgeon performs a difficult operation
n = 10 times.
•
X is the number of times that the operation is
a success.
•
The success rate for the operation is 80%. In
this case p = 0.80 and
•
X has a Binomial distribution with n = 10 and
p = 0.80.
10 
x
10 x


px    0.80 0.20
x
Computing p(x) for x = 1, 2, 3, … , 10
x
p (x )
x
p (x )
0
0.0000
6
0.0881
1
0.0000
7
0.2013
2
0.0001
8
0.3020
3
0.0008
9
0.2684
4
0.0055
10
0.1074
5
0.0264
The Graph
0.4
p (x )
0.3
0.2
0.1
0
1
2
3
4
5
6
7
Number of successes, x
8
9
10
Computing the summary parameters for the distribution –
m, s2, s
x
0
1
2
3
4
5
6
7
8
9
10
Total
p (x )
0.0000
0.0000
0.0001
0.0008
0.0055
0.0264
0.0881
0.2013
0.3020
0.2684
0.1074
1.000
xp(x)
0.000
0.000
0.000
0.002
0.022
0.132
0.528
1.409
2.416
2.416
1.074
8.000
 xp(x)
x2
x 2 p(x)
0
1
4
9
16
25
36
49
64
81
100
0.000
0.000
0.000
0.007
0.088
0.661
3.171
9.865
19.327
21.743
10.737
65.600
2
x
 p( x)
• Computing the mean:
m   xpx   8.0
x
• Computing the variance:


s 2   x  m 2 px 
2
x


2
  x px   xpx 
x
x

 65.6  8.0  1.60
2
• Computing the standard deviation:
s  s2
 1.25  1.118