Chapter Seven
... The width of the 90% confidence interval for μ is smaller than that of the 95% confidence interval. This is so because the value of t for a 90% confidence level is smaller than that for a 95% confidence level (with df remaining the same). ...
... The width of the 90% confidence interval for μ is smaller than that of the 95% confidence interval. This is so because the value of t for a 90% confidence level is smaller than that for a 95% confidence level (with df remaining the same). ...
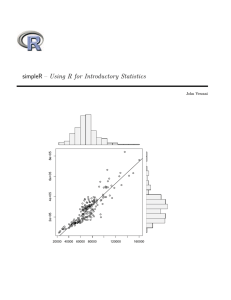
Verzani SimpleR
... and multiplication that make it easy to work with data when they are vectors. Let’s see how these apply to our typos example. First, suppose these are the typos for the first draft of section 1 of these notes. We might want to keep track of our various drafts as the typos change. This could be done ...
... and multiplication that make it easy to work with data when they are vectors. Let’s see how these apply to our typos example. First, suppose these are the typos for the first draft of section 1 of these notes. We might want to keep track of our various drafts as the typos change. This could be done ...
Objective Bayesian point and region estimation in location-scale models Jos´e M. Bernardo
... loss in terms of σ2 , the Bayes estimator is the mode of the posterior distribution of σ2 , π(σ2 | x) = π(σ | x)/(2σ), which is Mo(σ2 | x) = σ̃2n+1 , the same as (8), while the Bayes estimator for the zero-one loss in terms of σ is Mo(σ | x) = s, the MLE of σ, whose square is obviously not the same ...
... loss in terms of σ2 , the Bayes estimator is the mode of the posterior distribution of σ2 , π(σ2 | x) = π(σ | x)/(2σ), which is Mo(σ2 | x) = σ̃2n+1 , the same as (8), while the Bayes estimator for the zero-one loss in terms of σ is Mo(σ | x) = s, the MLE of σ, whose square is obviously not the same ...
chapter 8—interval estimation - College of Micronesia
... a. it is impossible to develop an interval estimate b. the standard deviation is arrived at using the range c. the sample standard deviation can be used d. it is assumed that the population standard deviation is 1 ANS: C ...
... a. it is impossible to develop an interval estimate b. the standard deviation is arrived at using the range c. the sample standard deviation can be used d. it is assumed that the population standard deviation is 1 ANS: C ...
Standard Deviation Calculator
... Confidence Limits Tab – Confidence Limits of the Standard Deviation Often, you will obtain an estimate of the standard deviation from a previous study or a pilot study. Since this estimate is based on a sample, it is important to understand its precision. This can easily be calculated since the squa ...
... Confidence Limits Tab – Confidence Limits of the Standard Deviation Often, you will obtain an estimate of the standard deviation from a previous study or a pilot study. Since this estimate is based on a sample, it is important to understand its precision. This can easily be calculated since the squa ...
Chapter 7 notes
... Copyright © 2007 Pearson Education, Inc Publishing as Pearson Addison-Wesley. ...
... Copyright © 2007 Pearson Education, Inc Publishing as Pearson Addison-Wesley. ...
Chapter 7
... Based on the survey results, we are 95% confident that the limits of 47.6% and 54.4% contain the true percentage of adult Minnesotans opposed to the photo-cop. The percentage of opposed adult Minnesotans is likely to be any value between 47.6% and 54.4%. However, a majority requires a percentage gre ...
... Based on the survey results, we are 95% confident that the limits of 47.6% and 54.4% contain the true percentage of adult Minnesotans opposed to the photo-cop. The percentage of opposed adult Minnesotans is likely to be any value between 47.6% and 54.4%. However, a majority requires a percentage gre ...
Section 6-1, 6-2
... Copyright © 2007 Pearson Education, Inc Publishing as Pearson Addison-Wesley. ...
... Copyright © 2007 Pearson Education, Inc Publishing as Pearson Addison-Wesley. ...
Bootstrapping (statistics)

In statistics, bootstrapping can refer to any test or metric that relies on random sampling with replacement. Bootstrapping allows assigning measures of accuracy (defined in terms of bias, variance, confidence intervals, prediction error or some other such measure) to sample estimates. This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods. Generally, it falls in the broader class of resampling methods.Bootstrapping is the practice of estimating properties of an estimator (such as its variance) by measuring those properties when sampling from an approximating distribution. One standard choice for an approximating distribution is the empirical distribution function of the observed data. In the case where a set of observations can be assumed to be from an independent and identically distributed population, this can be implemented by constructing a number of resamples with replacement, of the observed dataset (and of equal size to the observed dataset).It may also be used for constructing hypothesis tests. It is often used as an alternative to statistical inference based on the assumption of a parametric model when that assumption is in doubt, or where parametric inference is impossible or requires complicated formulas for the calculation of standard errors.