1.1 Descriptive Statistics
... numerical measures computed from a sample are called sample statistics while those numerical measures computed from a population are called population ...
... numerical measures computed from a sample are called sample statistics while those numerical measures computed from a population are called population ...
1 N SAMPLING DISTRIBUTION
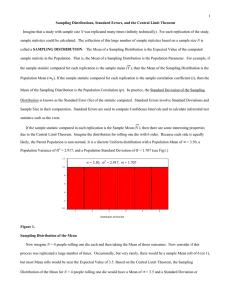
... and thus, theoretical sampling distributions are derived mathematically. The derivation usually comes from some form of the normal curve (another mathematically derived function); thus, no actual data are used to develop these distributions. Therefore, it is important to recognize that inferential s ...
... and thus, theoretical sampling distributions are derived mathematically. The derivation usually comes from some form of the normal curve (another mathematically derived function); thus, no actual data are used to develop these distributions. Therefore, it is important to recognize that inferential s ...
Data Analysis 1
... separates the critical region from the values of the test statistic that would lead us to reject the null hypothesis, this will depend on – the type of hypothesis (one or two tailed) – the sampling distribution (normal or skewed) – the level of significance (type of possible error and consequence) ...
... separates the critical region from the values of the test statistic that would lead us to reject the null hypothesis, this will depend on – the type of hypothesis (one or two tailed) – the sampling distribution (normal or skewed) – the level of significance (type of possible error and consequence) ...
Introductory Statistics – 4930AS
... (i) Using your table in (h), calculate the mean and standard deviation of the grouped data, correct to two decimal places. (j) Are your answers to (i) different from those in (f)? Why? (k) Add a column to your table in (i) for cumulative frequency. (l) Draw a cumulative frequency histogram and polyg ...
... (i) Using your table in (h), calculate the mean and standard deviation of the grouped data, correct to two decimal places. (j) Are your answers to (i) different from those in (f)? Why? (k) Add a column to your table in (i) for cumulative frequency. (l) Draw a cumulative frequency histogram and polyg ...
Chapter 3: Describing Relationships (first spread)
... these cards to the box and shuffle the cards in the box thoroughly. Draw another random sample of size 4, record the numbers, and find x . Repeat this as many times as is convenient, preferably about 100 times. Make a dotplot of the x -values and find their mean and standard deviation. This is an ap ...
... these cards to the box and shuffle the cards in the box thoroughly. Draw another random sample of size 4, record the numbers, and find x . Repeat this as many times as is convenient, preferably about 100 times. Make a dotplot of the x -values and find their mean and standard deviation. This is an ap ...
srs.pdf
... and Tn+1 . Implicitly, we are saying that if we had one additional data value we would compute Tn+1 (x1 , . . . , xn+1 ) rather than Tn (x1 , . . . , xn ), and if the entire population were available we would compute TN (x1 , . . . , xN ). It is therefore natural to require that the sequence of func ...
... and Tn+1 . Implicitly, we are saying that if we had one additional data value we would compute Tn+1 (x1 , . . . , xn+1 ) rather than Tn (x1 , . . . , xn ), and if the entire population were available we would compute TN (x1 , . . . , xN ). It is therefore natural to require that the sequence of func ...
Hypothesis Testing for the Proportion of Two Samples
... Hypothesis Testing for the Mean of Two Matched Pairs Note: This test requires that paired data are already listed in the STATDISK data window. If the data are not already there, close this window and enter or open data sets so that they are listed in columns of the STATDISK Data Window. (To open a d ...
... Hypothesis Testing for the Mean of Two Matched Pairs Note: This test requires that paired data are already listed in the STATDISK data window. If the data are not already there, close this window and enter or open data sets so that they are listed in columns of the STATDISK Data Window. (To open a d ...
Survival Statistics handout
... Knowing a measured standard deviation we would like t be able to state the exact uncertainty in our answer. Strictly speaking, we are not able to do this. Instead we can calculate a range of uncertainty at a given probability level, ( Sort of like gambling) and this is what the confidence interval ( ...
... Knowing a measured standard deviation we would like t be able to state the exact uncertainty in our answer. Strictly speaking, we are not able to do this. Instead we can calculate a range of uncertainty at a given probability level, ( Sort of like gambling) and this is what the confidence interval ( ...
Syllabus
... Standard deviation and variance for a population (a measure of distance from the mean) Step 1. The first step in finding the standard distance from the mean is to determine the deviation for each individual score. Deviation is the distance from the mean Deviation score = X - µ ...
... Standard deviation and variance for a population (a measure of distance from the mean) Step 1. The first step in finding the standard distance from the mean is to determine the deviation for each individual score. Deviation is the distance from the mean Deviation score = X - µ ...
Chapter Solutions
... b. The mode is the value that occurs most often. For data grouped into a frequency distribution, the mode is the midpoint of the class containing the most observations. There are more observations (12) in the $12 up to $14 class than in any other class. The midpoint of the class is $13, which is the ...
... b. The mode is the value that occurs most often. For data grouped into a frequency distribution, the mode is the midpoint of the class containing the most observations. There are more observations (12) in the $12 up to $14 class than in any other class. The midpoint of the class is $13, which is the ...
Bootstrapping (statistics)

In statistics, bootstrapping can refer to any test or metric that relies on random sampling with replacement. Bootstrapping allows assigning measures of accuracy (defined in terms of bias, variance, confidence intervals, prediction error or some other such measure) to sample estimates. This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods. Generally, it falls in the broader class of resampling methods.Bootstrapping is the practice of estimating properties of an estimator (such as its variance) by measuring those properties when sampling from an approximating distribution. One standard choice for an approximating distribution is the empirical distribution function of the observed data. In the case where a set of observations can be assumed to be from an independent and identically distributed population, this can be implemented by constructing a number of resamples with replacement, of the observed dataset (and of equal size to the observed dataset).It may also be used for constructing hypothesis tests. It is often used as an alternative to statistical inference based on the assumption of a parametric model when that assumption is in doubt, or where parametric inference is impossible or requires complicated formulas for the calculation of standard errors.