sampling distribution
... of sample means for a relatively simple, specific situation. In most cases, however, it will not be possible to list all the samples and compute all the possible sample means. Therefore, it is necessary to develop the general characteristics of the distribution of sample means that can be applied in ...
... of sample means for a relatively simple, specific situation. In most cases, however, it will not be possible to list all the samples and compute all the possible sample means. Therefore, it is necessary to develop the general characteristics of the distribution of sample means that can be applied in ...
Joint probability distributions
... distribution with population mean 22.40 cm and population standard deviation 0.03 cm. Cylinders for this type of engine have diameters that are also distributed normally, with mean 22.50 cm and standard deviation 0.04 cm. What is the probability that a randomly chosen piston will fit inside a random ...
... distribution with population mean 22.40 cm and population standard deviation 0.03 cm. Cylinders for this type of engine have diameters that are also distributed normally, with mean 22.50 cm and standard deviation 0.04 cm. What is the probability that a randomly chosen piston will fit inside a random ...
Slide 1
... If a variable is normally distributed, 68% of the cases (2/3) lie between plus and minus 1 standard deviation from the distribution’s mean, and 95% of the cases will lie between 1.96 standard deviations above and below the mean. ...
... If a variable is normally distributed, 68% of the cases (2/3) lie between plus and minus 1 standard deviation from the distribution’s mean, and 95% of the cases will lie between 1.96 standard deviations above and below the mean. ...
Topic 1_Statistical Analysis
... of course not arbitrary with a line graph. In this example, there are error bars for the individual samples. The samples are also connected by straight lines; they could also be connected by spline curves, which would give a smoother appearance, but which are no better predictors of intermediate val ...
... of course not arbitrary with a line graph. In this example, there are error bars for the individual samples. The samples are also connected by straight lines; they could also be connected by spline curves, which would give a smoother appearance, but which are no better predictors of intermediate val ...
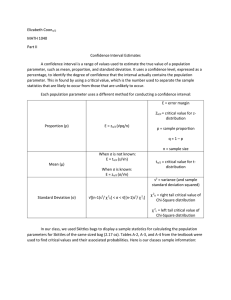
Confidence Interval Estimation Confidence Intervals on and μ
... • Confidence intervals assume that the sample means ...
... • Confidence intervals assume that the sample means ...
Confidence Intervals Review
... standard deviation of 0.085 ounces. Calculate and interpret a 99% confidence interval to estimate the true mean contents of the cans being filled by this machine. ...
... standard deviation of 0.085 ounces. Calculate and interpret a 99% confidence interval to estimate the true mean contents of the cans being filled by this machine. ...
As a condition of employment, Fashion Industries
... may not be reasonable to conclude that more than 10% are now failing the test. (b) Here it is given that, The sample proportion, p = 14/400 = 0.035 and q = 1 - p = 0.965 Now, the standard error SE = Sqrt(pq/n) ...
... may not be reasonable to conclude that more than 10% are now failing the test. (b) Here it is given that, The sample proportion, p = 14/400 = 0.035 and q = 1 - p = 0.965 Now, the standard error SE = Sqrt(pq/n) ...
CHAPTER EIGHT
... people travel more than 3500 miles between oil changes. A random sample of 8 cars getting an oil change has a mean distance of 3375 miles since the last oil change with a standard deviation of 225 miles. At alpha = 0.05, do you have enough evidence to support the shop’s claim? ...
... people travel more than 3500 miles between oil changes. A random sample of 8 cars getting an oil change has a mean distance of 3375 miles since the last oil change with a standard deviation of 225 miles. At alpha = 0.05, do you have enough evidence to support the shop’s claim? ...
Exam 1
... From the confidence interval results we know that with 95% assurance the slope is in the range [-0.243,-0.029], in particular at least with 95% assurance the slope is negative. Comment: Even though the R-square is relatively small, this only casts doubt on the predicted values of slope and intercept ...
... From the confidence interval results we know that with 95% assurance the slope is in the range [-0.243,-0.029], in particular at least with 95% assurance the slope is negative. Comment: Even though the R-square is relatively small, this only casts doubt on the predicted values of slope and intercept ...
Bootstrapping (statistics)

In statistics, bootstrapping can refer to any test or metric that relies on random sampling with replacement. Bootstrapping allows assigning measures of accuracy (defined in terms of bias, variance, confidence intervals, prediction error or some other such measure) to sample estimates. This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods. Generally, it falls in the broader class of resampling methods.Bootstrapping is the practice of estimating properties of an estimator (such as its variance) by measuring those properties when sampling from an approximating distribution. One standard choice for an approximating distribution is the empirical distribution function of the observed data. In the case where a set of observations can be assumed to be from an independent and identically distributed population, this can be implemented by constructing a number of resamples with replacement, of the observed dataset (and of equal size to the observed dataset).It may also be used for constructing hypothesis tests. It is often used as an alternative to statistical inference based on the assumption of a parametric model when that assumption is in doubt, or where parametric inference is impossible or requires complicated formulas for the calculation of standard errors.