Uranium-238 Decay Series
... Uranium, a radioactive element, decays to the stable element lead-206 by emitting alpha particle or beta particles. Use the periodic table to dentify the elements by the number of proton in the nucleus. Remember the atomic mass is the sum of protons and neutrons. Complete the following chart by foll ...
... Uranium, a radioactive element, decays to the stable element lead-206 by emitting alpha particle or beta particles. Use the periodic table to dentify the elements by the number of proton in the nucleus. Remember the atomic mass is the sum of protons and neutrons. Complete the following chart by foll ...
CHAPTER 1. SPECIAL RELATIVITY AND QUANTUM MECHANICS 1.1 PARTICLES AND FIELDS §
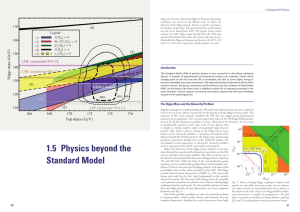
... energies around 10 eV, that is to describe experiments dealing with atomic distances comparable to the Bohr radius aBohr = h̄2 /me2 = 0.5 × 10−8 cm , can, when combined with special relativity, provide a correct description of nature at distance scales a billion times shorter! The origins of quantum ...
... energies around 10 eV, that is to describe experiments dealing with atomic distances comparable to the Bohr radius aBohr = h̄2 /me2 = 0.5 × 10−8 cm , can, when combined with special relativity, provide a correct description of nature at distance scales a billion times shorter! The origins of quantum ...
A Primer on Quantum Mechanics and Orbitals
... Where E is a number not a function (in this case total energy). Note that in equations like this after the application of the operator (in this case H, the Hamiltonian operator) to the wavefunction you get the eigenvalue (E) and the same wavefunction back. In the case we looked at above (the momentu ...
... Where E is a number not a function (in this case total energy). Note that in equations like this after the application of the operator (in this case H, the Hamiltonian operator) to the wavefunction you get the eigenvalue (E) and the same wavefunction back. In the case we looked at above (the momentu ...
Symmetry: a bridge between nature and culture
... worlds has required no language other than that of ordinary geometry. Then, were we transported to those worlds, there would be no need to change that language. Beings educated there would no doubt find it more convenient to create a geometry different from ours, and better adapted to their impressi ...
... worlds has required no language other than that of ordinary geometry. Then, were we transported to those worlds, there would be no need to change that language. Beings educated there would no doubt find it more convenient to create a geometry different from ours, and better adapted to their impressi ...
Generation of twin-photons in triple microcavities
... applications. A vertical triple microcavity consists in three coupled planar microcavities, optically strongly coupled via 2 intermediate Bragg mirrors so that the electro-magnetic field is delocalized throughout the full nanostructure. At resonance between the three cavities, the cavity mode degene ...
... applications. A vertical triple microcavity consists in three coupled planar microcavities, optically strongly coupled via 2 intermediate Bragg mirrors so that the electro-magnetic field is delocalized throughout the full nanostructure. At resonance between the three cavities, the cavity mode degene ...
Comparison of 3D classical and quantum mechanical He scattering
... of the wave number vector k parallel to the surface is shorter than 3.74 a.u. on the contrary when the He atom is near the top layer of the Rh(3 1 1) surface. The attractive part of the interaction potential leads to longer lifetime near the ...
... of the wave number vector k parallel to the surface is shorter than 3.74 a.u. on the contrary when the He atom is near the top layer of the Rh(3 1 1) surface. The attractive part of the interaction potential leads to longer lifetime near the ...
Time-Independent Perturbation Theory Atomic Physics Applications 1 Introduction
... We only have time to touch on atomic physics in this course, and we will focus only on the hydrogen atom for the time-being. This ignores the important and rich problem of electron-electron interaction, which dominates most of the periodic table of elements. The results from studying hydrogen, howev ...
... We only have time to touch on atomic physics in this course, and we will focus only on the hydrogen atom for the time-being. This ignores the important and rich problem of electron-electron interaction, which dominates most of the periodic table of elements. The results from studying hydrogen, howev ...
Effective Field Theory Lectures
... The uncertainty principle tells us that to probe the physics of short distances we need high momentum. On the one hand this is annoying, since creating high relative momentum in a lab costs a lot of money! On the other hand, it means that we can have predictive theories of particle physics at low en ...
... The uncertainty principle tells us that to probe the physics of short distances we need high momentum. On the one hand this is annoying, since creating high relative momentum in a lab costs a lot of money! On the other hand, it means that we can have predictive theories of particle physics at low en ...
SuperKEKB - grapes-3
... Lies a sophisticated vertexing and inner tracking system (VXD) to: • Determine the vertex position of the weakly decaying particles • Precisely measure the track position and momentum for low-pT tracks ...
... Lies a sophisticated vertexing and inner tracking system (VXD) to: • Determine the vertex position of the weakly decaying particles • Precisely measure the track position and momentum for low-pT tracks ...
general properties of the solution: quantum numbers:
... quantum number is sufficient to describe the solution - a particle in a 3D box requires three quantum numbers for the specification of its wave function because of the three independent boundary conditions - the electron in the hydrogen atom is confined by a 3D potential generated by the nucleus - t ...
... quantum number is sufficient to describe the solution - a particle in a 3D box requires three quantum numbers for the specification of its wave function because of the three independent boundary conditions - the electron in the hydrogen atom is confined by a 3D potential generated by the nucleus - t ...
Renormalization

In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities.Renormalization specifies relationships between parameters in the theory when the parameters describing large distance scales differ from the parameters describing small distances. Physically, the pileup of contributions from an infinity of scales involved in a problem may then result in infinities. When describing space and time as a continuum, certain statistical and quantum mechanical constructions are ill defined. To define them, this continuum limit, the removal of the ""construction scaffolding"" of lattices at various scales, has to be taken carefully, as detailed below.Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory. Initially viewed as a suspect provisional procedure even by some of its originators, renormalization eventually was embraced as an important and self-consistent actual mechanism of scale physics in several fields of physics and mathematics. Today, the point of view has shifted: on the basis of the breakthrough renormalization group insights of Kenneth Wilson, the focus is on variation of physical quantities across contiguous scales, while distant scales are related to each other through ""effective"" descriptions. All scales are linked in a broadly systematic way, and the actual physics pertinent to each is extracted with the suitable specific computational techniques appropriate for each.