assignment 2.
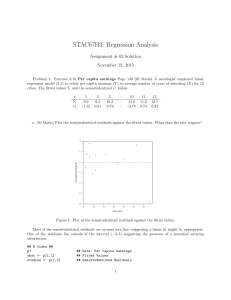
... More or less, a linear relation appears to be reasonable for the two variables. ## R Codes ## x <- c(0:9) y <- c(98, 135, 162, 178, 221, 232, 283, 300, 374, 395) plot(x, y, xlab = "Year", ylab = "Sales in thousands of units") reg <- lm(y ~ x) abline(reg) b. [15 Marks] Use the Box-Cox procedure and s ...
... More or less, a linear relation appears to be reasonable for the two variables. ## R Codes ## x <- c(0:9) y <- c(98, 135, 162, 178, 221, 232, 283, 300, 374, 395) plot(x, y, xlab = "Year", ylab = "Sales in thousands of units") reg <- lm(y ~ x) abline(reg) b. [15 Marks] Use the Box-Cox procedure and s ...
EIB E213: Econometrics The Fletcher School, Tufts University Fall 2013
... Reading an econometrics text is never easy, but it is essential that you make the effort to read this book. In the past, students have primarily relied upon the notes and not used the book (and many students will probably tell you not to purchase the book). This is your opportunity to learn the “wri ...
... Reading an econometrics text is never easy, but it is essential that you make the effort to read this book. In the past, students have primarily relied upon the notes and not used the book (and many students will probably tell you not to purchase the book). This is your opportunity to learn the “wri ...
Analysis of Traffic Accidents before and after resurfacing - A statistical approach
... periods. The chi-squared distribution is used to test the findings. I have also aimed at finding an appropriate Poisson regression model using SAS procedure which could well explain the expected number of accidents depending on different explanatory variables. Key words: Traffic Accidents, Statistic ...
... periods. The chi-squared distribution is used to test the findings. I have also aimed at finding an appropriate Poisson regression model using SAS procedure which could well explain the expected number of accidents depending on different explanatory variables. Key words: Traffic Accidents, Statistic ...
MA111 - Mohawk Valley Community College
... fundamentals and usefulness of exploring relationships among quantitative variables for the purposes of model building and prediction. Student Outcomes: ...
... fundamentals and usefulness of exploring relationships among quantitative variables for the purposes of model building and prediction. Student Outcomes: ...
Diagnosing Diabetes Type II Using a Soft Intelligent
... Although many different approaches exist in order to find the optimal architecture of an artificial neural network, these methods are usually quite complex in nature and are difficult to implement (Zhang & Patuwo, 1998). Furthermore, none of these methods can guarant ...
... Although many different approaches exist in order to find the optimal architecture of an artificial neural network, these methods are usually quite complex in nature and are difficult to implement (Zhang & Patuwo, 1998). Furthermore, none of these methods can guarant ...
Standardized binomial models for risk or prevalence ratios and
... Joint Effects of Two Exposures Suppose that there are two exposure variables of interest, E and F. Assessment of whether there is a departure from additivity of effects may be of interest, for example to evaluate whether an intervention on E would have a larger absolute effect jointly with exposure ...
... Joint Effects of Two Exposures Suppose that there are two exposure variables of interest, E and F. Assessment of whether there is a departure from additivity of effects may be of interest, for example to evaluate whether an intervention on E would have a larger absolute effect jointly with exposure ...
Innovations and Applications in Quantitative Research
... (CDF) function. Nominal/dichotomous and ordinal measures use the probit, logistic or log-log link function to map to a CDF. Uses prior probability of each category given little/no ...
... (CDF) function. Nominal/dichotomous and ordinal measures use the probit, logistic or log-log link function to map to a CDF. Uses prior probability of each category given little/no ...
p - HKUST Business School
... On the other hand, people often put too much reliance on the precise numbers. In the debate over climate change, the tendency is to state all the uncertainties and caveats associated with the climate model projections -- and then forget about them, said Dr. Steve Rayner, a specialist in global clima ...
... On the other hand, people often put too much reliance on the precise numbers. In the debate over climate change, the tendency is to state all the uncertainties and caveats associated with the climate model projections -- and then forget about them, said Dr. Steve Rayner, a specialist in global clima ...
Selectivity Estimation using Probabilistic Models
... The probability that two tuples join with each other can also be correlated with various attributes. ...
... The probability that two tuples join with each other can also be correlated with various attributes. ...
Lecture01
... have pdfs. In the next lecture, though, we are going to eliminate the distinction between the two in order to simplify notation and also in order to allow us to talk about variables that are partly continuous and discrete. Every random variable will have a pdf. These turn out to be very useful and w ...
... have pdfs. In the next lecture, though, we are going to eliminate the distinction between the two in order to simplify notation and also in order to allow us to talk about variables that are partly continuous and discrete. Every random variable will have a pdf. These turn out to be very useful and w ...
Linear regression
In statistics, linear regression is an approach for modeling the relationship between a scalar dependent variable y and one or more explanatory variables (or independent variables) denoted X. The case of one explanatory variable is called simple linear regression. For more than one explanatory variable, the process is called multiple linear regression. (This term should be distinguished from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable.)In linear regression, data are modeled using linear predictor functions, and unknown model parameters are estimated from the data. Such models are called linear models. Most commonly, linear regression refers to a model in which the conditional mean of y given the value of X is an affine function of X. Less commonly, linear regression could refer to a model in which the median, or some other quantile of the conditional distribution of y given X is expressed as a linear function of X. Like all forms of regression analysis, linear regression focuses on the conditional probability distribution of y given X, rather than on the joint probability distribution of y and X, which is the domain of multivariate analysis.Linear regression was the first type of regression analysis to be studied rigorously, and to be used extensively in practical applications. This is because models which depend linearly on their unknown parameters are easier to fit than models which are non-linearly related to their parameters and because the statistical properties of the resulting estimators are easier to determine.Linear regression has many practical uses. Most applications fall into one of the following two broad categories: If the goal is prediction, or forecasting, or error reduction, linear regression can be used to fit a predictive model to an observed data set of y and X values. After developing such a model, if an additional value of X is then given without its accompanying value of y, the fitted model can be used to make a prediction of the value of y. Given a variable y and a number of variables X1, ..., Xp that may be related to y, linear regression analysis can be applied to quantify the strength of the relationship between y and the Xj, to assess which Xj may have no relationship with y at all, and to identify which subsets of the Xj contain redundant information about y.Linear regression models are often fitted using the least squares approach, but they may also be fitted in other ways, such as by minimizing the ""lack of fit"" in some other norm (as with least absolute deviations regression), or by minimizing a penalized version of the least squares loss function as in ridge regression (L2-norm penalty) and lasso (L1-norm penalty). Conversely, the least squares approach can be used to fit models that are not linear models. Thus, although the terms ""least squares"" and ""linear model"" are closely linked, they are not synonymous.























