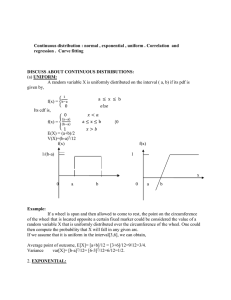
Logistic Regression
... • Learns the Conditional Probability Distribution P(y|x) • Local Search. – Begins with initial weight vector. – Modifies it iteratively to maximize an objective function. – The objective function is the conditional log likelihood of the data – so the algorithm seeks the probability distribution P(y| ...
... • Learns the Conditional Probability Distribution P(y|x) • Local Search. – Begins with initial weight vector. – Modifies it iteratively to maximize an objective function. – The objective function is the conditional log likelihood of the data – so the algorithm seeks the probability distribution P(y| ...
Regression Line and Prediction. - Department of Mathematics and
... ⇒ A regression line summarizes the relationship between two variables in the setting when one of the variables helps explain or predict the other. ⇒ Regression describes a relationship between an explanatory variables and a response variable. Regression Line A regression line is a straight line that ...
... ⇒ A regression line summarizes the relationship between two variables in the setting when one of the variables helps explain or predict the other. ⇒ Regression describes a relationship between an explanatory variables and a response variable. Regression Line A regression line is a straight line that ...
MISCELLANEOUS REGRESSION TOPICS
... The variance of Y at this value of X can be shown to be p(X)(1 - p(X)). i. Consequently, the variance of Y depends on the value of X. Normally, this variance will not be the same, a situation that violates the assumption of constant variance. ii. Recall the discussion and examples earlier in the cou ...
... The variance of Y at this value of X can be shown to be p(X)(1 - p(X)). i. Consequently, the variance of Y depends on the value of X. Normally, this variance will not be the same, a situation that violates the assumption of constant variance. ii. Recall the discussion and examples earlier in the cou ...
Multiple Correlation/ Regression as a Simplification of the GLM
... Although the model is linear, that is, specifies a straight line relationship between X and Y, it may be modified to test nonlinear models. For example, if you think that the function relating Y to X is quadratic, you employ the model Y a b1 X b2 X 2 e . It is often more convenient to work w ...
... Although the model is linear, that is, specifies a straight line relationship between X and Y, it may be modified to test nonlinear models. For example, if you think that the function relating Y to X is quadratic, you employ the model Y a b1 X b2 X 2 e . It is often more convenient to work w ...
Binomial (or Binary) Logistic Regression
... Yi = b0 + b1X1 + i b0: interception at y-axis b1: line gradient X1: predictor variable : Error X1 predicts Y. ...
... Yi = b0 + b1X1 + i b0: interception at y-axis b1: line gradient X1: predictor variable : Error X1 predicts Y. ...