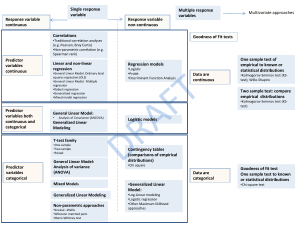
Advantages of Multivariate Analysis
... The variation of Y values around the regression line is a measure of how X and Y relate to each other. Method of quantifying the variation is by Analysis of variance presented as Analysis of Variance table Total sum of squares represents total variation of Y values around their mean - Syy ...
... The variation of Y values around the regression line is a measure of how X and Y relate to each other. Method of quantifying the variation is by Analysis of variance presented as Analysis of Variance table Total sum of squares represents total variation of Y values around their mean - Syy ...
The data for a Y-on-X regression problem come in the form (x1, Y1
... The values x1 , x 2 ,..., x n are known non-random quantities which are measured without error. If in fact the x values really are random, then we assume that they are fixed once we have observed them. This is a verbal sleight of hand; technically we say we are doing the analysis “conditional on the ...
... The values x1 , x 2 ,..., x n are known non-random quantities which are measured without error. If in fact the x values really are random, then we assume that they are fixed once we have observed them. This is a verbal sleight of hand; technically we say we are doing the analysis “conditional on the ...
Section 9.2, Linear Regression
... In Section 9.1, we calculated that r = −0.969, so r2 = .939 and 93.9% of the variation is explained by the regression line (and 6.1% is due to random and unexplained factors). 2. A study involved comparing the per capita income (in thousands of dollars) to the number of medical doctors per 10,000 r ...
... In Section 9.1, we calculated that r = −0.969, so r2 = .939 and 93.9% of the variation is explained by the regression line (and 6.1% is due to random and unexplained factors). 2. A study involved comparing the per capita income (in thousands of dollars) to the number of medical doctors per 10,000 r ...