MODIFIED MERSENNE NUMBERS AND PRIMES Several thousand
... super-composites typically have exponent vectors of the form [k1 k2 k3 ….0 0 0] with k1>k2>k3.Typically the number of non-vanishing ks will be small. Let us demonstrate. Consider the super-compositeS=2160=25·33·52 whose exponent vector reads [5 3 2 0 0 0] If we look at S-1=2159 and S+1=2161, we find ...
... super-composites typically have exponent vectors of the form [k1 k2 k3 ….0 0 0] with k1>k2>k3.Typically the number of non-vanishing ks will be small. Let us demonstrate. Consider the super-compositeS=2160=25·33·52 whose exponent vector reads [5 3 2 0 0 0] If we look at S-1=2159 and S+1=2161, we find ...
Notes on Factors, Prime Numbers, and Prime
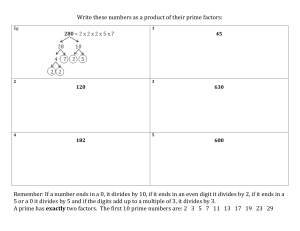
... A number with three or more factors is a composite number. Divisibility rules can be used to factor a number and to test the primality of a number. Some divisibility rules: • All numbers are divisible by 1 • Any even number is divisible by 2. A number is divisible by 2 if it ends with a 0, 2, 4, 6, ...
... A number with three or more factors is a composite number. Divisibility rules can be used to factor a number and to test the primality of a number. Some divisibility rules: • All numbers are divisible by 1 • Any even number is divisible by 2. A number is divisible by 2 if it ends with a 0, 2, 4, 6, ...
Number Theory
... • There are infinitely many primes. • Primes do thin out as numbers get bigger: o The density of primes < 2 digit numbers is 1 / 4. o The density of primes < 3 digit numbers is 1 / 6. o The density of primes < 10 digit numbers is 1 / 23. o The density of primes < 100 digit numbers is 1 / 230. In gen ...
... • There are infinitely many primes. • Primes do thin out as numbers get bigger: o The density of primes < 2 digit numbers is 1 / 4. o The density of primes < 3 digit numbers is 1 / 6. o The density of primes < 10 digit numbers is 1 / 23. o The density of primes < 100 digit numbers is 1 / 230. In gen ...
Intro to public-key ciphers A symmetric or private
... But observe that knowledge of the RSA modulus n = pq and of m = (p − 1)(q − 1) would amount to knowing the factors p, q, since the roots of the polynomial equation X 2 + (m − n + 2)X + n = 0 are p, q. Presumably factoring is hard, so this is evidence (?) that an eavesdropper will not find a trick wh ...
... But observe that knowledge of the RSA modulus n = pq and of m = (p − 1)(q − 1) would amount to knowing the factors p, q, since the roots of the polynomial equation X 2 + (m − n + 2)X + n = 0 are p, q. Presumably factoring is hard, so this is evidence (?) that an eavesdropper will not find a trick wh ...
Number Theory Integer Division I Integer Division II Integer Division
... Take note of the difference between the two problems—primality is a decision problem; we try to determine if the answer is “yes” or “no”. However, factorization is a functional problem, we are actually trying to find a number; a factor. Numerous algorithms for primality testing have been developed o ...
... Take note of the difference between the two problems—primality is a decision problem; we try to determine if the answer is “yes” or “no”. However, factorization is a functional problem, we are actually trying to find a number; a factor. Numerous algorithms for primality testing have been developed o ...