Lecture 12
... Ground state of hydrogen: it has one proton with spin I=1/2 and one electron with spin J=1/2 (orbital angular momentum is zero). What is the total angular momentum F of the ...
... Ground state of hydrogen: it has one proton with spin I=1/2 and one electron with spin J=1/2 (orbital angular momentum is zero). What is the total angular momentum F of the ...
Chapter 6
... Symbolized by ms Indicates the fundamental spin states of an electron in an orbital Values are + ½ and -1/2 ...
... Symbolized by ms Indicates the fundamental spin states of an electron in an orbital Values are + ½ and -1/2 ...
1. Crystal Properties and Growth of Semiconductors
... radiation emanating from them Bohr postulates: 1) Electron exists in certain stable circular orbits about the nucleus and does not give off radiation 2) Electron may shift to an orbit of higher or lower energy by absorbing or emitting a photon of energy hf 3) Angular momentum is quantized p =m v r = ...
... radiation emanating from them Bohr postulates: 1) Electron exists in certain stable circular orbits about the nucleus and does not give off radiation 2) Electron may shift to an orbit of higher or lower energy by absorbing or emitting a photon of energy hf 3) Angular momentum is quantized p =m v r = ...
SIMULATION PRODUCTS AND THE MULTI
... Atoms comprise all matter within our universe, and define the nature and properties inherent to our existence. An atom is made up of a positively charged central nucleus surrounded by one or more negatively charged electrons, which occupy a distinct space, or orbital, dependent upon their energies. ...
... Atoms comprise all matter within our universe, and define the nature and properties inherent to our existence. An atom is made up of a positively charged central nucleus surrounded by one or more negatively charged electrons, which occupy a distinct space, or orbital, dependent upon their energies. ...
Light and quantized Energy Section 1
... several unexplainable phenomena (photoelectric effect) but not why atomic emission spectra of elements were discontinuous rather continuous. ...
... several unexplainable phenomena (photoelectric effect) but not why atomic emission spectra of elements were discontinuous rather continuous. ...
Energy Sublevels
... Uncertainty Principle 1927 - Heisenberg proposed what he is most well Known for … The Uncertainty Principle “It is impossible to simultaneously know both the Position and Velocity (a vector) of a particle at the ...
... Uncertainty Principle 1927 - Heisenberg proposed what he is most well Known for … The Uncertainty Principle “It is impossible to simultaneously know both the Position and Velocity (a vector) of a particle at the ...
02 Atomic Structure
... Q 17. The mass of electron moving with the velocity of light is: (a) 2me (b) 3me (c) zero (d) Can be calculated as by formula ...
... Q 17. The mass of electron moving with the velocity of light is: (a) 2me (b) 3me (c) zero (d) Can be calculated as by formula ...
ppt
... theory – Elements are composed of atoms – Atoms of the same element are Billard Ball identical, each element is unique – Compounds are composed of atoms Model of more than 1 element, atoms combine in fixed ratios to form compounds – Chemical rxn involves separation, combination, or rearrangement of ...
... theory – Elements are composed of atoms – Atoms of the same element are Billard Ball identical, each element is unique – Compounds are composed of atoms Model of more than 1 element, atoms combine in fixed ratios to form compounds – Chemical rxn involves separation, combination, or rearrangement of ...
Orbital
... Electronic transitions in the Bohr model for the hydrogen atom. (a) An energy-level diagram for electronic transitions. (b) an orbittransition diagram, which accounts for the experimental spectrum. (Note that the orbits shown are schematic. They are not drawn to scale.) (c) The resulting line spectr ...
... Electronic transitions in the Bohr model for the hydrogen atom. (a) An energy-level diagram for electronic transitions. (b) an orbittransition diagram, which accounts for the experimental spectrum. (Note that the orbits shown are schematic. They are not drawn to scale.) (c) The resulting line spectr ...
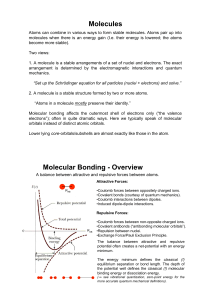
Molecules Molecular Bonding
... 1. A molecule is a stable arrangements of a set of nuclei and electrons. The exact arrangement is determined by the electromagnetic interactions and quantum mechanics. “Set up the Schrödinger equation for all particles (nuclei + electrons) and solve.” 2. A molecule is a stable structure formed by tw ...
... 1. A molecule is a stable arrangements of a set of nuclei and electrons. The exact arrangement is determined by the electromagnetic interactions and quantum mechanics. “Set up the Schrödinger equation for all particles (nuclei + electrons) and solve.” 2. A molecule is a stable structure formed by tw ...
Unit 5 Notes - Har
... Orientation around the nucleus (x, y, z planes) Spin state (+1/2 or -1/2) ...
... Orientation around the nucleus (x, y, z planes) Spin state (+1/2 or -1/2) ...
Chapter 5
... Lowest energy to higher energy. Adding electrons can change the energy of the orbital. Half filled orbitals have a lower energy. Makes them more stable. Changes the filling order ...
... Lowest energy to higher energy. Adding electrons can change the energy of the orbital. Half filled orbitals have a lower energy. Makes them more stable. Changes the filling order ...
EMR and the Bohr Model of the Atom
... • All matter exhibits both particle and wave properties. • Large pieces of matter (i.e. baseball) exhibits mostly particle properties. • Tiny pieces of matter (i.e. photons) exhibits mostly wave properties. • Pieces of matter somewhere in the middle (i.e. electrons) clearly show both types of proper ...
... • All matter exhibits both particle and wave properties. • Large pieces of matter (i.e. baseball) exhibits mostly particle properties. • Tiny pieces of matter (i.e. photons) exhibits mostly wave properties. • Pieces of matter somewhere in the middle (i.e. electrons) clearly show both types of proper ...
CHAPTER 5 NOTES – ELECTRONS IN ATOMS
... to another energy level • Quantum Mechanical Model – the modern description of the electron in atoms – from the mathematical solutions to the Schrödinger equation – determines the allowed energies an electron can have and how likely it is to find the electron in various locations around the nucleus ...
... to another energy level • Quantum Mechanical Model – the modern description of the electron in atoms – from the mathematical solutions to the Schrödinger equation – determines the allowed energies an electron can have and how likely it is to find the electron in various locations around the nucleus ...
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus. The term may also refer to the physical region or space where the electron can be calculated to be present, as defined by the particular mathematical form of the orbital.Each orbital in an atom is characterized by a unique set of values of the three quantum numbers n, ℓ, and m, which respectively correspond to the electron's energy, angular momentum, and an angular momentum vector component (the magnetic quantum number). Any orbital can be occupied by a maximum of two electrons, each with its own spin quantum number. The simple names s orbital, p orbital, d orbital and f orbital refer to orbitals with angular momentum quantum number ℓ = 0, 1, 2 and 3 respectively. These names, together with the value of n, are used to describe the electron configurations of atoms. They are derived from the description by early spectroscopists of certain series of alkali metal spectroscopic lines as sharp, principal, diffuse, and fundamental. Orbitals for ℓ > 3 continue alphabetically, omitting j (g, h, i, k, …).Atomic orbitals are the basic building blocks of the atomic orbital model (alternatively known as the electron cloud or wave mechanics model), a modern framework for visualizing the submicroscopic behavior of electrons in matter. In this model the electron cloud of a multi-electron atom may be seen as being built up (in approximation) in an electron configuration that is a product of simpler hydrogen-like atomic orbitals. The repeating periodicity of the blocks of 2, 6, 10, and 14 elements within sections of the periodic table arises naturally from the total number of electrons that occupy a complete set of s, p, d and f atomic orbitals, respectively.