![Weak measurements [1] Pre and Post selection in strong measurements](http://s1.studyres.com/store/data/008913441_1-7a0f5f5a1778eb5da686e2de8a47882f-300x300.png)
Discussion of Experimental Proof for the Paradox of Einstein, Rosen
... First of all, Bohr' has proposed that the observing apparatus plus what is observed form a single indivisible combined system not capable at the quantummechanical level of being analyzed correctly into separate and distinct parts. Each particular kind of apparatus then forms with an electron for exa ...
... First of all, Bohr' has proposed that the observing apparatus plus what is observed form a single indivisible combined system not capable at the quantummechanical level of being analyzed correctly into separate and distinct parts. Each particular kind of apparatus then forms with an electron for exa ...
lecture31
... There are four different quantum numbers needed to specify the state of an electron in an atom: 1) Principal quantum number n gives the total energy: ...
... There are four different quantum numbers needed to specify the state of an electron in an atom: 1) Principal quantum number n gives the total energy: ...
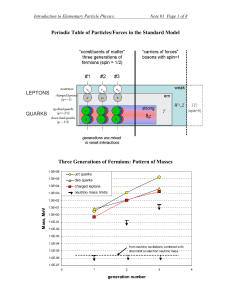
Periodic Table of Particles/Forces in the Standard Model
... three kinematical (meter, second, kilogram) and one electrical (Ampere1) It is common in the realm of the elementary particle physics to redefine units so that speed of light and Plank’s constant become equal to one: c=1 and ℏ =1. This imposes two constraints on the three kinematical units and, ther ...
... three kinematical (meter, second, kilogram) and one electrical (Ampere1) It is common in the realm of the elementary particle physics to redefine units so that speed of light and Plank’s constant become equal to one: c=1 and ℏ =1. This imposes two constraints on the three kinematical units and, ther ...
Tunneling between Edge States in a Quantum Spin Hall System
... but can instead be characterized by a topological quantity [1,2]. The importance of being able to identify a phase of quantum matter that does not fall under the GinzburgLandau paradigm has set off a search for other topologically nontrivial states, analogous to, but distinct from those connected to ...
... but can instead be characterized by a topological quantity [1,2]. The importance of being able to identify a phase of quantum matter that does not fall under the GinzburgLandau paradigm has set off a search for other topologically nontrivial states, analogous to, but distinct from those connected to ...
Molekylfysik - Leiden Institute of Physics
... The spin “s” of a particle is an angular momentum characterizing the rotation (the spinning) of the particle around its own axis. The wavefunction of the particle has to satisfy specific boundary conditions for this motion (not the same as for the 3D-rotation). It follows that this spin angular mo ...
... The spin “s” of a particle is an angular momentum characterizing the rotation (the spinning) of the particle around its own axis. The wavefunction of the particle has to satisfy specific boundary conditions for this motion (not the same as for the 3D-rotation). It follows that this spin angular mo ...
Document
... • The rules for determining the ground-state quantum numbers for LS coupling atoms are known as Hund’s rules. – For a given electron configuration, the state with maximum multiplicity (2S+1) lies lowest in energy. – For a given multiplicity (S), the state with the largest value of L lies lowest in i ...
... • The rules for determining the ground-state quantum numbers for LS coupling atoms are known as Hund’s rules. – For a given electron configuration, the state with maximum multiplicity (2S+1) lies lowest in energy. – For a given multiplicity (S), the state with the largest value of L lies lowest in i ...
Electrons as waves
... • De Broglie pointed out that in many ways the behavior of the Bohr’s quantized electron orbits was similar to the known behavior of waves. • Electrons should be thought of as having a dual wave-particle nature also. ...
... • De Broglie pointed out that in many ways the behavior of the Bohr’s quantized electron orbits was similar to the known behavior of waves. • Electrons should be thought of as having a dual wave-particle nature also. ...
Spin Qubits for Quantum Information Processing
... for nuclear spins and electron spins in solids and liquids was dated back to early 1940s [1]. The first nuclear magnetic resonance (NMR) experiments were performed independently by E.M. Purcell’s group at Harvard [2] and by F. Bloch’s group at Stanford [3] in 1946. The first electron spin resonance ...
... for nuclear spins and electron spins in solids and liquids was dated back to early 1940s [1]. The first nuclear magnetic resonance (NMR) experiments were performed independently by E.M. Purcell’s group at Harvard [2] and by F. Bloch’s group at Stanford [3] in 1946. The first electron spin resonance ...
β - Indico
... 5. Aharonov Y., Cohen E., Elitzur A.C. (2012), Coexistence of past and future measurements’ effects, predicted by the Two-State-Vector-Formalism and revealed by weak measurement. Submitted to Phys. Rev. A. http://arxiv.org/abs/1207.0667 . 6. Aharonov Y., Cohen E., Grossman D., Elitzur A.C. (2012), C ...
... 5. Aharonov Y., Cohen E., Elitzur A.C. (2012), Coexistence of past and future measurements’ effects, predicted by the Two-State-Vector-Formalism and revealed by weak measurement. Submitted to Phys. Rev. A. http://arxiv.org/abs/1207.0667 . 6. Aharonov Y., Cohen E., Grossman D., Elitzur A.C. (2012), C ...
Derivation of the Pauli exchange principle
... where x is a set of space coordinates, and s represents a set of spin quantum numbers. Pauli [1] showed that this relation connecting fermion and boson statistics with spin can be derived with the aid of relativistic quantum field theory. As will be seen below, it can also be derived directly from t ...
... where x is a set of space coordinates, and s represents a set of spin quantum numbers. Pauli [1] showed that this relation connecting fermion and boson statistics with spin can be derived with the aid of relativistic quantum field theory. As will be seen below, it can also be derived directly from t ...