PHYS 215: Introductory Quantum Physics January
... topics covered correspond to chapter 1, a brief review of relativistic energy and momentum from chapter 2, chapters 3, 4, 5, 6, and if time allows part of chapter 7. Required courses Prerequisites: Pre- or co-requisites: ...
... topics covered correspond to chapter 1, a brief review of relativistic energy and momentum from chapter 2, chapters 3, 4, 5, 6, and if time allows part of chapter 7. Required courses Prerequisites: Pre- or co-requisites: ...
One-entangled-evening-JP
... The protected “logical” quantum information is encoded in a highly entangled state of many physical qubits. The environment can't access this information if it interacts locally with the protected system. ...
... The protected “logical” quantum information is encoded in a highly entangled state of many physical qubits. The environment can't access this information if it interacts locally with the protected system. ...
Landau Levels and Quantum Group
... theories and integrable lattice models [4]. Although the abelian ChernSimons theory does not possess a quantum group structure in the literature [3], it might be possible to exhibit one in some other senses. There have been also interesting investigations of condensed matter problems such as the fra ...
... theories and integrable lattice models [4]. Although the abelian ChernSimons theory does not possess a quantum group structure in the literature [3], it might be possible to exhibit one in some other senses. There have been also interesting investigations of condensed matter problems such as the fra ...
Q 19: Quantum Optics III - DPG
... includes several quite large optical elements which makes it difficult to use and combine them in compact quantum computational circuits. Technologies that allow to realise quantum optical functionalities in small integrated systems are much more promising in this respect. In this work we present a ...
... includes several quite large optical elements which makes it difficult to use and combine them in compact quantum computational circuits. Technologies that allow to realise quantum optical functionalities in small integrated systems are much more promising in this respect. In this work we present a ...
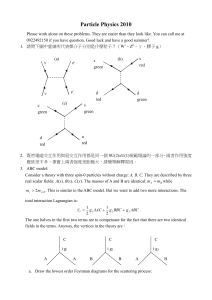
Particle Physics
... of a Klein-Gordon Field. The second and third term could be considered as the negative of the potential. Since the Lagrangian is composed only of the inner products of 3 vectors, it is invariant under O(3), ie. the 3D rotation. The Hamiltonian can be written as ...
... of a Klein-Gordon Field. The second and third term could be considered as the negative of the potential. Since the Lagrangian is composed only of the inner products of 3 vectors, it is invariant under O(3), ie. the 3D rotation. The Hamiltonian can be written as ...
Research Overview -JEJ Last Colloquium Spring 2009.ppt
... space time is that one adds sequentially (with decreasing importance) new dimensions (4*(2n1)) to space-time (giving it an extra 4, 12…dimensions) with some topological constraints that are complicated. These are analogous to the ground state energies (e.g. as with the harmonic oscillator) due to th ...
... space time is that one adds sequentially (with decreasing importance) new dimensions (4*(2n1)) to space-time (giving it an extra 4, 12…dimensions) with some topological constraints that are complicated. These are analogous to the ground state energies (e.g. as with the harmonic oscillator) due to th ...
Lecture Notes, Feb 24, 2016
... 1, 2, 3.... as shown in Fig. (3) The integer n is called quantum number. • For H-atom, the energies of these electrons is En = −13.6/n2 13.6 comes from a constant that is determined by Planck constant and mass and charge of the electron ( 13.6 = Ke4 me /h2 , where K is a constant that determines the ...
... 1, 2, 3.... as shown in Fig. (3) The integer n is called quantum number. • For H-atom, the energies of these electrons is En = −13.6/n2 13.6 comes from a constant that is determined by Planck constant and mass and charge of the electron ( 13.6 = Ke4 me /h2 , where K is a constant that determines the ...
Document
... Dark fringe: (x,y,z,t)2 small , possibility small 。 (x,y,z,t)2 is proportion to possibility density in this point. ...
... Dark fringe: (x,y,z,t)2 small , possibility small 。 (x,y,z,t)2 is proportion to possibility density in this point. ...
Erwin Schroedinger, Max Born and Wave Mechanics
... Was awarded the Nobel Prize in Physics for 1932 "for the creation of quantum mechanics". Studied physics under Max Born and soon became his assistant Most famous for his discovery of The uncertainty principle which says that you cannot measure the position (x) and the momentum (p) of a particle with ...
... Was awarded the Nobel Prize in Physics for 1932 "for the creation of quantum mechanics". Studied physics under Max Born and soon became his assistant Most famous for his discovery of The uncertainty principle which says that you cannot measure the position (x) and the momentum (p) of a particle with ...