Download Resistance Across Cubic Network

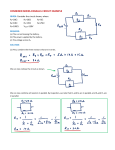
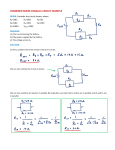
Resistance Across Cubic Network
A------B
/|
/|
D------C |
| E----|-F
|/
|/
H------G
Each of the twelve edges of the cube is
a resistor of value R.
What is the resistance between points
A and G?
How can I do this?
If all of the resistors are identical, then there is a quick way to
find the equivalent resistance of the cube network. To do this, you
simply insert additional wires between points that you know to be at
the same voltage.
A------B
/|
/|
D------C |
| E----|-F
|/
|/
H------G
Each of the twelve edges of the cube is
a resistor of value R.
What is the resistance between points
A and G?
In this network, the points B, D, and E are equivalent, i.e., all of
them have the same voltage, namely exactly one resistance drop down
from the voltage at point A. Thus, we may connect these three points
together by wires BD, DE, and BE without changing anything.
Similarly, the points F, H, and C are equivalent, and we may connect
them together with wires.
Now imagine shrinking these wire loops down to a single point. This
collapses together the points BDE and CFH. The circuit now looks like
this (when flattened out):
/-R-\
/--R--\
-R/
\
/---R---\
/
\
o---A---R--(BCD)----R--(CFH)--R--G---o
\
/
\---R---/
\
/
--R-\--R--/
-R--R--
Thus, this cube network is equivalent to the series combination of
three things: a set of 3 resistors in parallel, a set of 6 resistors
in parallel, and another set of 3 resistors in parallel. Thus the
total equivalent resistance of the cube from A to G is
R_total = (R/3) + (R/6) + (R/3) = R(1/3 + 1/6 + 1/3) = 5R/6.
Note that the key idea is to notice that you can connect equivalent
voltages in a circuit by a wire without changing the current flow, so
that the overall properties of the circuit remain unchanged. This is
possible when all of the resistors are the same.
When the resistors are not all the same, one may have to resort to
Kirchoff's Laws, which keep track of the currents in the loops and
the voltages at the nodes of any circuit network. You are probably
familiar with the formulas for series and parallel resistances:
R[series] = R1 + R2
and
R[parallel] = 1/[1/R1 + 1/R2].
These formulas are shortcuts for replacing a small network of
resistors with an equivalent effective resistance. Kirchhoff's laws
are used to derive these transformations, which are useful because the
series and parallel combinations occur often in real circuits.
Another transformation that is sometimes useful, but less commonly
seen, is the delta-wye transformation:
X--Rxy--Y
\
/
Rxz
Ryz
\ /
Z
X
<---->
"delta"
\
Rx
Y
/
Ry
\ /
|
Rz
|
"wye"
Z
The formulas that relate these resistances are
Rxy = (RxRy + RyRz + RzRx)/Rz
Ryz = (RxRy + RyRz + RzRx)/Rx
Rxz = (RxRy + RyRz + RzRx)/Ry
"wye to delta"
Rx = RxyRxz/(Rxy + Ryz + Rxz)
Ry = RxyRyz/(Rxy + Ryz + Rxz)
Rz = RxzRyz/(Rxy + Ryz + Rxz)
"delta to wye"
Sometimes using these equations are useful for simplifying a circuit
without going through all of the equations from Kirchhoff's Laws.