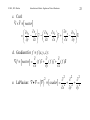Download Review of Matrix Algebra

 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
1
Matrix Operations
Matrix - a collection of numbers or other items arranged in a
particular manner in an array.
Rectangular Matrix - array with n rows and m columns)
 a11 a12 a13 ... a1m 
a

a
a
...
a
23
2m 
 21 22
[ A]   a31 a32 a33
a3m 

( nxm ) 
...
 ...

 an1 an 2 an3 ... anm 
aij = term in row i and column j
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
Column Matrix – only 1 column in the matrix (sometimes
called a column vector)
 b1 
 b1 
b 
b 
 2
or [ B ]   2 
{B}   
( nx1)  ... 
( nx1)  ... 
 
bn 
bn 
Row Matrix – only 1 row in the matrix (sometimes called a
row vector)
[C ]  [c1 c2 ... cn ]
(1xn )
2
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
Matrix Addition
3
[C ]  [ A]  [ B]
( nxm )
( nxm ) ( nxm )
cij  aij  bij
[A] and [B] must be the same size!
Matrix Multiplication
[C ]  [ A] [ B]
( nxm )
( nxp ) ( pxm)
i  1, 2,..., n
cij   aik bkj 
 j  1, 2,...m
k 1
p
The number of columns
in [A] (i.e., p) must be
equal to the number of
rows in [B].
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
4
The definition of cij is equivalent to taking the dot product of
row i of matrix [A] and column j of matrix [B].
If [A] is (2x4) and [B] is (4x3):
 a11 a12
[ A]  
 a21 a22
a13
a23
 b11
b
a14 
 21
and
[
B
]

a24 
b31

b41
b12
b22
b32
b42
b13 
b23 

b33 

b43 
4
then,
c23   a2 k bk 3
k 1
 a21b13  a22b23  a23b33  a24b43
Pictorially, called “row into column multiplication”
 2001, W.E. Haisler
 c11 c12
c
 21 c22
Introduction to Matrix Algebra and Vector Mechanics
c13   a11 a12


c23   a21 a22
a13
a23
 b11
a14  b21


a24  b31

b41
5
b12
b22
b32
b42
b13 
b23 

b33 

b43 
Note: In general, matrix multiplication is not commutative,
i.e., [ A][ B]  [ B][ A]
Matrix Division – NOT DEFINED! Instead the matrix
inverse [ A]1 is defined. If [ A][ B]  [ I ] where [I] is the
identity matrix (all zeros except for 1’s on main diagonal
running from upper left to lower right), then [ B]  [ A]1 such
that [ A][ A]1  [ I ].
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
Transpose Matrix – Given [A], then the transpose is given
by [ A]T and is formed by interchanging all rows with
corresponding columns. An (nxm) matrix becomes an (mxn)
matrix.
Symmetric Matrix – A matrix is symmetric about its main
diagonal (diagonal running from upper left to lower right) if
aij  a ji . For example, for a (3x3), we
 3 1 2 
have 9 values, but the 3 values below
 1 6 4 
[
A
]

the diagonal are equal to the


 2 4 5 
corresponding 3 values above the
diagonal; hence, only 6 unique values
due to the symmetry.
6
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
System of n Equations –
a11x1 a12 x2 ...  a1n xn  c1
a21x1 a22 x2 ...  a2 n xn  c2
...
an1x1 an 2 x2 ...  ann xn  cn
or, in matrix notation:
 a11 a12 ... a1n   x1   c1 
a
  x  c 
a
...
a
2n   2   2 
 21 22
     or [A]{X}={C}
 ...
  ...   ... 

   
 an1 an 2 ... ann   xn  cn 
7
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
Vector Operations & Operators
Scalar Product (also called dot or inner product)
a. Definitions: Given: two vectors A and B ,

D  A  B  A B cos
A
D = A  B  a x bx  a y by  az bz

 B
b. Observations
1) Vector  Vector  Scalar (one order down from a
vector)
2) Vector  Matrix (second order tensor)  Vector
(one order down from a second order tensor)
3) The dot product ALONE is commutative &
distributive
8
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
A B  B  A

9

A B  C  A B  AC
Note: if one of the quantities in a dot product has
differentiation in it, the commutative property of the
dot product will not hold.
4) ADVANTAGE of 2nd definition of dot product?
Do not have to evaluate magnitude of vectors, i.e. do
not have to calculate the following:
A  a x2  a 2y  a z2
5) Physical meaning? Projection of one directional
quantity (vector, second order tensor, or higher tensor)
on to another directional quantity (vector, second order
tensor, or higher tensor)
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
10
6) USES:
a. Find the angle between two vectors
b. Find the magnitude of the projection of one vector
onto another (parallel component)
c. Determines orthogonality (dot product = zero, then
orthogonal)
What does A  B really mean in terms of how it is evaluated?
It is very similar to algebraic multiplication. For example, if
you have the algebraic product (ax  a y  az )(bx  by  bz ) ,
you get 9 terms in the product:
axbx  a y bx  a z bx
 a x by  a y by  a z by
 axbz  a y bz  az bz
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
If you have the vector product
(ax i  a y j  az k )  (bx i  by j  bz k )
you still get nine terms but they include the unit vectors and
the dot product operator:
axbx i  i  a y bx j  i  a z bx k  i
 a x by i  j  a y by j  j  a z by k  j
 axbz i  k  a y bz j  k  az bz k  k
 axbx  a y by  az bz
11
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
12
Cross Product
a. Definition:
i
j
k
C  A  B  ax
ay
az
bx
by
bz
i

ay
az
by
bz
j
ax
az
bx
bz
k
ax
ay
bx
by



 a y bz  a z by i   a xbz  a z bx  j  a xby  a ybz k


b. Alternate approach: C  A B sin A, B (a scalar not
a vector, direction comes from right hand rule)
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
c. Observations
1) Physical meaning? C is normal () to
the plane defined by A & B
13
C
B
A
2) Commutative property does not hold
3) Distributive property does hold
4) USES:
a. Magnitude of Cross Product is the area of the
parallelogram mapped by the two vectors
b. Calculates Moments: M  R  F
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
14
Dyadic Product (also called outer, tensor, or vector product)
a. Definition:
The dyadic product means
that you are multiplying
a i 
 x 
the 3 components of A
AB  a y j  bx i by j bz k 
times the 3 components of


B (like algebra) and then
a
k
 z 
 a xbx ii

  a y bx ji

 a z bx ki
a xby ij
a y by jj
a z by kj
a xbz ik 

a ybz jk 

a z bz kk 
arranging results into a
(3x3) matrix.
This is called a Tensor because each term has two unit vectors.
Notice: Two Unit Vectors accompany each entry.
First Unit Vector denotes face (on a cube).
Second Unit Vector denotes direction of vector.
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
15
b. Observations
1) No “vector operator” between vectors (though
sometimes the  symbol is used, i.e., A  B )
2) VECTOR times VECTOR  Matrix (2nd Order
Tensor)
3) Note matrix representation: {3x1}[1x3] gives a
[3x3] by distributing each component of the first
vector over the second vector to form the three “rows”
of the matrix representation of the second order tensor
4) USES:
a. Stress is a Tensor
b. Strain is a Tensor
c. Dot products between vectors and second order tensors
is given by
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
 Txx i i

T  v = Tyx j i

Tzx k i
Txz ik   v x i 
 

Tyy jj Tyz jk    v y j 

 
Tzy kj Tzz kk   v z k 
Txy ij
(Txx v x  Txy v y  Txz v z )i 


  (Tyx v x  Tyy v y  Tyz v z ) j 


 (Tzx v x  Tzy v y  Tzz v z )k 
 The above dot product means that 9 quantities are
dotted with 3 quantities.
 You get 27 terms. However, 18 of these disappear
(because i  j  0 , etc.), so only 9 terms are left.
 Arrange 9 terms as a (3x3 matrix).
16
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
1) Vector operation is just like a matrix operation in
this case, i.e., calculations are done by “row down
column” method which yields a vector
2) E.g. #1 (Second Unit Vector of Tensor Dots with
Unit Vector of Vector leaving First Unit Vector of
Tensor to form the New Vector)
3) E.g. #2 (Unit Vector of Vector Dots with First
Unit Vector of Tensor leaving Second Unit Vector of
Tensor to form the New Vector)
Suppose you have v  T instead. Using same procedure to
take the dot product, you obtain:
17
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
v  T =  v x i
 Txx i i

v y j v z k   Tyx j i

Tzx k i
18
Txz ik 

Tyy jj Tyz jk 

Tzy kj Tzz kk 
Txy ij
(v x Txx  v yTyx  v z Tzx )i 


  (v x Txy  v yTyy  v z Tyz ) j 


 (v x Txz  v yTyz  v z Tzz )k 
Note that a tensor is denoted by two arrows above it, i.e., T .
While the dot product of a vector and a vector yields a
scalar, the dot product of a vector and a tensor yields a
vector.
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
19
Differential Operators
1. Derivatives (Review of Calculus I)
a. Total derivative: Given:
 f x x   f x  
df
f  f  x  , then f   x  
 lim 

dx x0 
x

f ( x  x )
f ( x)
x
x
x  x
Physical meaning? Slope of line
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
20
b. Partial Derivatives
1) Given: f  f  x, y 
 f x x, y   f x, y  
f
 lim 
 (holding y constant)
x x0 
x

 f x, y y   f x, y  
f
 lim 
 (holding x constant)
y y 0 
y

2)
Example: f  x, y   A  Bx  Cy  Dxy  Ex 2  Fy 2
3)
f
 slope with respect to x at a fixed y
Physically,
x
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
21
2.
Del Operator (Review of Calculus II and III)



j k
a. Definition:   i 
x
y
z
i.e., “A differential vector” in Cartesian coordinates
b. Divergence (of B):
 

 
  B   scalar    i 
j  k   bxi  by j  bz k
y
z 
 x

bx by bz



x
y
z
Note that B   yields a completely different result:

 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
22
 

 
B     vector   bxi  by j  bz k   i 
j k
y
z 
 x
by
bx

 bx
 by
 bz
x
y
z


The above is a vector operator just like  is a vector
operator.
Hence, when you take the dot product of two vector AND
one of the vectors is an operator (like  ), you cannot
interchange the order of operation (like you can with a
simple dot product).
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
23
c. Curl:
  V   vector 
 vz v y   vx vz 
 v y vx 




i  
k
 j 
z   z
x 
y 
 y
 x
d. Gradient for f  f ( x, y, z ) :



f   vector   ( f )i  ( f ) j  ( f )k
x
y
z
2
2
2
    scalar   x2  y 2  y 2
e. LaPlacian:     
2
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
24
ASIDE: Review of Unit Vectors
A. Definition: a vector whose magnitude is one.
Given: a  axi  a y j  az k
Then: a is a unit vector if: a  1  ax2  a 2y  az2
B. Examples:
1. Is this a unit vector:
b i  j k
b  12  12  12  3  1
2. Is this a unit vector:
c j
c  12  1 Yes
 No
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
25
3. How would you make b  i  j  k a unit vector? Divide
by it’s magnitude:
1
1
1
b
i
j
k
3
3
3
2
2
2
3
 1   1   1 
b  
 
 
  3 1
 3  3  3
The symbol “^” is sometimes used over a vector to denote
a unit vector.
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
Determining normal to a plane
Recall equation of a plane:
Ax  By  Cz  D
Define f :
f  Ax  By  Cz  D  0
Gradient of f gives a normal
vector to the plane: n  f
n
Divide by the magnitude to get a unit normal: n 
n
Problem! You don’t know which direction the unit normal
points (into or out of plane surface).
26
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
Another approach. Define two
vectors A and B as shown. These
vectors obviously lie in the plane
of the surface. Do N  A  B .
This gives a vector perpendicular
to A and B (and the normal points
outward because of right hand
rule!), hence N  A  B is
perpendicular to the plane. The
B
27
A
N
unit normal to the surface is then given by n 
.
N
To find the component of vector t perpendicular to the
surface (i.e., in direction of n , do tn  n  t . The vector is
then given by tn  tn n
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
28
Angle between t and n can be found from tn  n  tn n cos
1  tn
n 
or   cos 
 tn n 


Important note. In the above, and on the following page,
when you determine the component of a vector (say t ) in the
direction of another vector (say n ) using the dot product,
THE VECTOR n MUST BE A UNIT VECTOR.
 2001, W.E. Haisler
Introduction to Matrix Algebra and Vector Mechanics
29
Determining components of a vector F that are normal and
parallel to a surface with unit vector n normal to the surface.

F
F
Fy

n
Fx
 = CCW angle from x-axis
Fp

Fn
y
x
The normal component is first obtained from the dot product
Fn  n  F
or as a vector
Fn  Fn n  (n  F )n
The parallel component is obtained from vector addition

F  Fn  Fp
Fp  F  Fn